“Specific heat capacity indicates the ability of a substance to store heat. This substance quantity corresponds to the amount of heat required to heat a given amount of a substance to one Kelvin.”
With the help of DSCs, the specific heat capacity (hereafter referred to as Cp) can be determined [3, Section 6.2]. The specific heat capacity, by adding mass, is an intensive quantity. It indicates how much heat a substance must absorb in order to increase the mass of a substance by a defined temperature difference. The Cp depends on the temperature and is calculated as follows
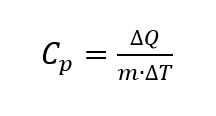
where the ambient pressure is assumed to be constant [2, p. 118]. The unit for the specific heat capacity [3, p. 78] is
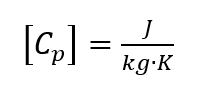
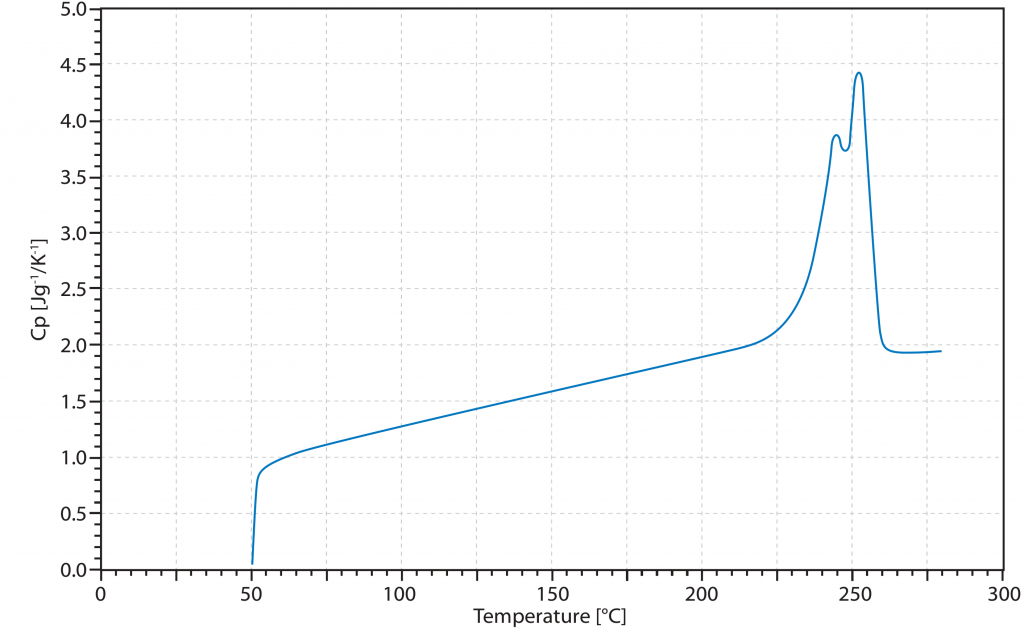
The reason for the increase in the Cp value shown is the endothermic character of this transition. This causes the measuring system to supply more energy in order to follow the given temperature profile. However, this does not correspond to the real Cp and for this reason the specific heat capacity in the region of a phase transition is assumed to be infinite.
Referencing using sapphire
Sapphire represents the most widely used standard for the determination of correction factors for the measurement of specific heat capacity with DSCs. The crystal, consisting of aluminum oxide (hereafter referred to as Al2O3), occurs in natural form. However, sapphire can also be produced synthetically and in perfect quality. Synthetically produced sapphire glasses are usually colorless and, due to their high melting temperature of 2050 °C, inert in the temperature range commonly used for DSCs. Artificial production allows sapphire to be manufactured with high accuracy and represents a very precise standard. However, samples with widely differing specific heat capacities may exhibit measurement deviations. In this case, a standard with a comparable specific heat capacity should be used.
Methods for determining specific heat capacity using DSC
There are various methods for determining specific heat capacity using differential scanning calorimeters. These are briefly presented below.
Classical CP measurement using DSC
The classical determination of the specific heat capacity by means of DSCs is carried out in three steps. In a first step, only the corresponding sample crucible is heated and thus the zero curve corresponding to the experiment is recorded in order to compensate for the inertia of the measuring system. In a second step, a known reference material is measured with the same experimental conditions. The prerequisite is that the material is very pure, well defined and inert in the desired temperature range. Likewise, literature values for the heat capacity of the reference material as a function of temperature must be available. In a third step, the sample to be investigated is measured under the same experimental conditions. The zero curve is subtracted in each case from the reference and sample measurements. From the difference between the two DSC curves, a calibration factor and comparison of the heat flows allow the determination of specific heat capacity to be calculated according to
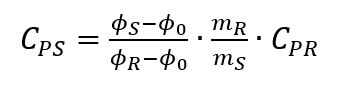
[4, p. 119]. An illustration of the three curves and the method can be seen in Fig. 2.
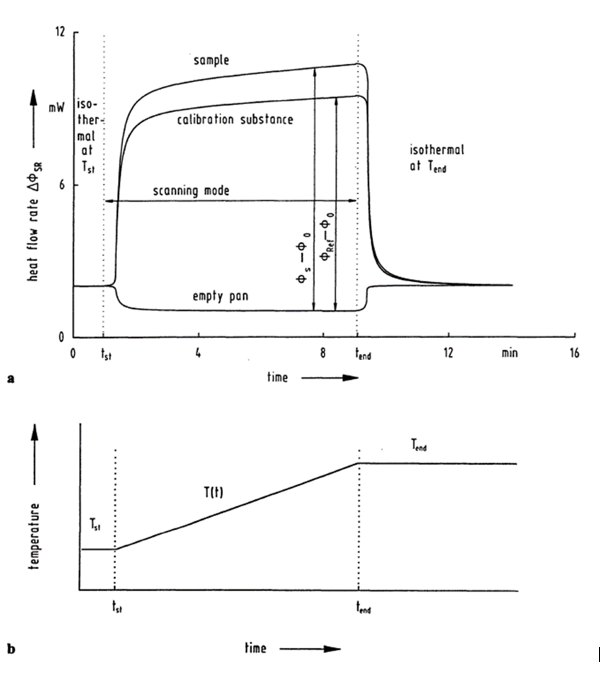
Since very small sample weights are used, it is necessary to determine the masses of reference material and sample very accurately. Crucibles and all other ambient conditions must be kept as identical as possible. Otherwise, measurement deviations will occur, so care must be taken to position the crucible and sample precisely. The reference material should also be similar to the sample under investigation in terms of initial weight and specific heat capacity in order to minimize influences such as temperature gradients across the sample.
Temperature-modulated CP measurement using DSC
When determining the specific heat capacity by means of temperature-modulated measurement, the temperature curve is superimposed by a sine wave. A prerequisite for this measurement method is that the DSC can follow the given modulated temperature. Accordingly, the temperature profile [4, p. 132] can be described as follows:
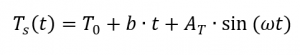
From this the heat flow results from
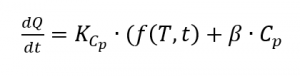
with
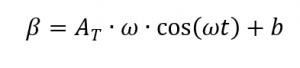
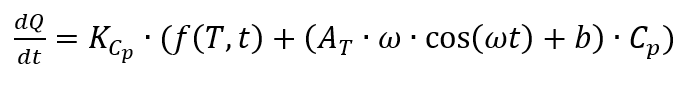
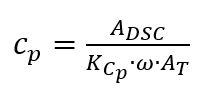
Temperature-modulated CP measurement using DSC
When determining the specific heat capacity by means of temperature-modulated measurement, the temperature curve is superimposed by a sine wave. A prerequisite for this measurement method is that the DSC can follow the given modulated temperature. Accordingly, the temperature profile [4, p. 132] can be described as follows:
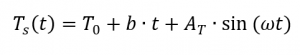
From this the heat flow results from
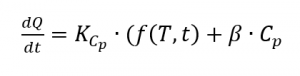
with
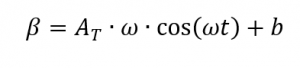
[2, p. 187] whereby applies
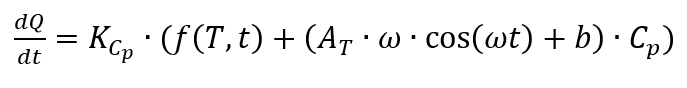
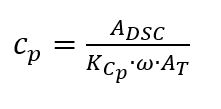
the inertia of the measuring systems and furnaces limits the amplitude and causes long periods. In order to obtain a good resolution of the resulting heat capacity, a sufficiently large number of modulation periods must be passed through, which means that measurements are time-consuming.
Separation of reversible and irreversible parts of the DSC signal
A DSC-signal can be divided into a reversible (abbreviated as REV in the following) and a non-reversible (abbreviated as NONREV in the following) part according to
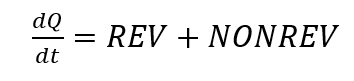
[5, p. 172]. The reversible part of a DSC signal includes those effects that occur reproducibly, such as glass transitions or melting processes [2, Chap. 3.1.4]. Irreversible effects are those that occur only once in the corresponding sample, such as the evaporation of water. With the help of temperature-modulated measurement, these signals can be separated from each other. According to the formula for calculating the temperature-modulated measurement [5, p. 172], it can be assumed that
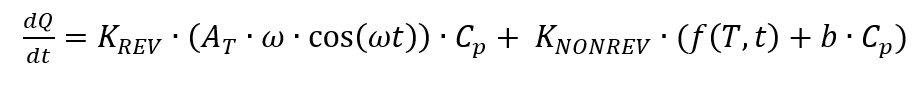
Accordingly, the reversible part can be described as follows.
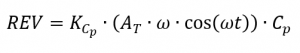
and the irreversible part of a DSC signal according to
If the modulated measurement signal was recorded and the specific heat capacity was calculated by means of DSC as under temperature modulated CP measurement, NONREV can be calculated according to
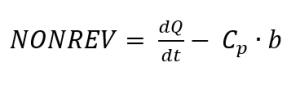
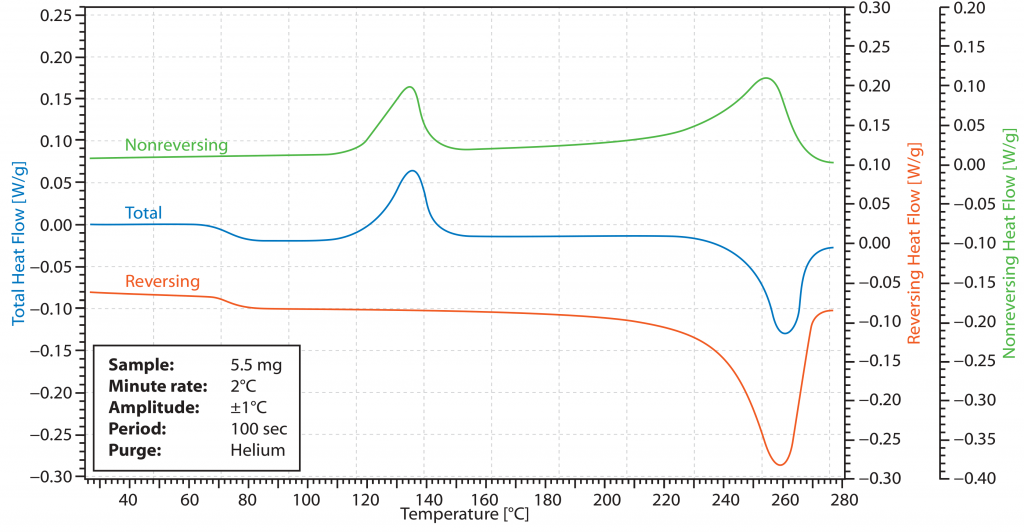
and thus REV can also be calculated by subtracting NONREV from the DSC signal. If effects are superimposed by others during measurements, they can often be clearly assigned and evaluated with the help of this separation. However, the time and effort required are significantly greater. Fig. 3 shows a typical representation of a DSC signal with the associated reversible and irreversible components.
3-Omega CP measurement by DSC
Another method for determining specific heat capacity is the 3ω-method. Invented by David Cahill, the method uses a heater excited with angular velocity ω. The method is actually used to determine the thermal conductivity [6, p. 19]. This is determined by
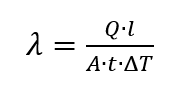
and can be used in conjunction with
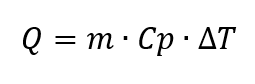
can be converted [6, p. 69]. Thus, by measuring the periodic temperature change on the sample, it is possible to determine how large the specific heat capacity is. However, since the method is designed to measure thin-film samples, which are rarely used in conventional DSC measurements, the method is hardly suitable for conventional DSC instruments.
You can determine the specific heat capacity with the following Linseis measuring instruments: Chip-DSC, DSC L62, STA
Literature:
- B. Wunderlich, Thermal Analysis of Polymeric Materials. Berlin, Heidelberg: Springer-Verlag Berlin Heidelberg, 2005.
- S. M. Sarge, G. W. H. Höhne und W. Hemminger, Calorimetry: Fundamentals, instrumentation and applications. Weinheim, Germany: Wiley-VCH Verlag, 2014.
- G. W. H. Höhne, W. Hemminger und H.-J. Flammersheim, Differential Scanning Calorimetry: An Introduction for Practitioners. Berlin, Heidelberg: Springer, 1996.
- G. W. H. Höhne, W. F. Hemminger und H.-J. Flammersheim, Differential Scanning Calorimetry, 2. Aufl. Berlin, Heidelberg: Springer, 2003.
J. D. Menczel und R. B. Prime, Thermal analysis of polymers. Hoboken, N.J: John Wiley, 2009. - P. Böckh und T. Wetzel, Wärmeübertragung: Grundlagen und Praxis, 5. Aufl. Berlin: Springer Vieweg, 2014.
