Determination of the CTE density
Contents:
- Thermal expansion and density
- Definition of thermal expansion
- Phase transformations
- Measurement of the expansion coefficient
- Liquids
- Solid body
Thermal expansion and density
The thermal expansion of materials can lead to great commercial damage. In construction, for example, expansion joints must be provided in order to compensate for changes in length in the event of temperature fluctuations. Furthermore, the coefficients of expansion of materials in contact must be matched to one another. If the coefficients of expansion of a ceramic body and a glazing differ too much, so-called “spiderweb cracks” are formed, which can often be observed on old porcelain plates.
The expansion takes place in all spatial directions, so that the density changes, since the mass remains constant. In the case of anisotropic materials, the expansion is direction-dependent, so that the direction of the expansion must be specified. Consequently, all spatial directions must be taken into account to determine the density or the volume expansion coefficient.
Definition of thermal expansion
The coefficient of thermal expansion (CTE) is defined as the relative change in length on a temperature change of one Kelvin:
α= ∆L/(L0 *∆T)
mit:
∆L: Length change [m]
L0: Output length [m]
∆T: Temperature change [K]
giving results in α units of K-1 (“per Kelvin”). It is temperature-dependent and therefore changes but often only to a small extent, depending on the temperature range under consideration. Its magnitude is typically 10-6 K-1 and is therefore often given in “ppm K-1”.
Materials with low expansion coefficients are, for example, quartz glass and the metal INVAR, which have an expansion coefficient of less than 1 ppm K-1. The largest coefficients of expansion have polymers (up to about 200 ppm K-1). Some materials have negative expansions, depending on the temperature range.
Phase transformations
Coefficients of expansion of different phases of the same material differ. For example, the coefficients of expansion of polymers above the glass transition temperature are greater than those below.
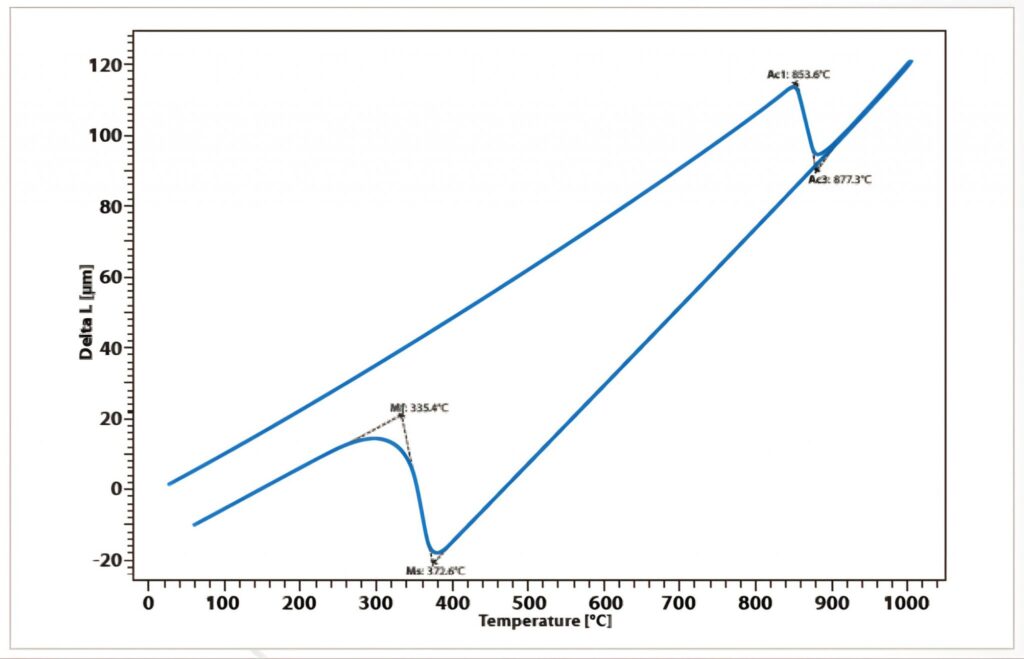
Another known example is the phase transformations of elemental iron: up to 90°C, the cubic-space-centered crystal structure is stable (α-iron), from 906°C to 1401°C, it has the most cubic density (β-iron), and above 1539°C again it returns to the cubic-space-centered crystal structure (δ-iron). Since the space filling of the most cubic-density packing (74%) is greater than that of the cubic-centered packing (68%), there are jumps in density and thus also in length in the phase transformations. These are used to detect phase transitions in iron alloys:
Measurement of the expansion coefficient
The measuring method to be selected depends on the state of aggregation of the sample, the size of the coefficient of expansion of the sample to be measured and the temperature range to be considered. The mechanical properties of the sample must also be taken into account in the production of suitable samples and thus in the selection of the measurement method.
Liquids
The expansion or density of liquids is generally determined by pycnometers. In this case, a constant volume of the sample is temperature-controlled and the mass is determined. Fluids usually expand with increasing temperature. A well-known exception is water which has its density maximum at 4 °C (“anomaly of water”).
Furthermore, the so-called bending oscillation method is used. In this case, the density is calculated from the measurement of the natural frequency of a bending oscillator filled with the liquid to be investigated.
Liquids can also be measured using suitable liquid containers on a push rod dilatometer. In this case, make sure that no gases escape from the liquid or escaping gases also leave the container, whereby, however, the liquid sample must not escape.
Solid body
Solids are usually measured using (push rod) dilatometers or thermo-mechanical analyzers (TMA). In this case, the sample is introduced into an oven, and contact is made with it using a push rod. The change in length of the sample is transmitted by the push rod to a sensor. Depending on the oven used, a temperature range of -263 to +2800°C can be covered. Depending on the temperature range, push rods made of quartz glass, aluminum oxide or graphite are used. Differential transformers (LVDT – linear variable differential transformers) and recently also optical encoders are mostly used as sensors.
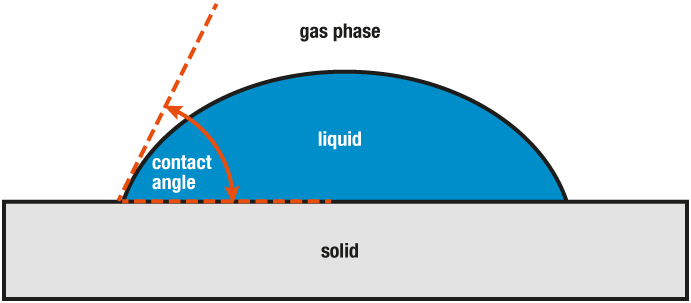
If the samples are difficult to process, fragile or easily deformable due to their properties, so that they do not withstand the force of the contacting push rod, optical dilatometers, also called heating microscopes, are used. Here, as in the case of the push rod dilatometer, the sample is placed in a furnace. The sample is observed using a camera whose images are measured. Through image analysis, not only the expansion (here even in 2 dimensions) but also changes in shape and melting can be observed and contact angles calculated.
Powdered samples are measured in special adapters. In this case, make sure that the enclosed air but not the sample, can escape (analogous to the measurement of liquids). The degree of compaction (bulk density, vibration density and tapped density) of the sample must also be observed: it must not be changed by the measurement conditions.
Materials with particularly low expansion coefficients are measured using interferometric methods. In this case, monochromatic light is reflected from the sample and brought to interference with a second beam (principle of the Michelson interferometer). The change in length results from the wavelength of the light used and the number of interferences. Such measuring devices are also called laser dilatometers.
