Table of Contents
What are thermoelectric materials?
Thermoelectric materials can convert heat directly into electrical energy. This property is based on the Seebeck effect, in which a temperature difference applied to a material generates a voltage. The reverse is the Peltier effect, which is usually used for cooling. A third thermoelectric effect is the Thomson effect, which describes the heat transport along a current-carrying conductor in which a temperature gradient exists.
Due to the possibility of directly using thermal energy, thermoelectric materials have become the focus of research and development. On the one hand, they can be used to generate electrical energy from primary energy sources; on the other hand, it is tempting to generate electricity from waste heat, thereby conserving fossil fuel resources and reducing the release of CO2 at the same time.
Since the electrical voltage induced by the Seebeck effect is very small (usually a few to a few hundred μV/K), great efforts are being made to develop improved thermoelectric materials.
Classic thermoelectric materials come from the group of semimetals and semiconductors (IV to VI main group of the periodic table) or are alloys of materials of these groups, since the Seebeck coefficient is particularly high there. The Seebeck effect can be further increased by doping.
What is the figure of merit?
In general, a figure of merit is a measure of the suitability of materials, methods, or equipment compared to alternatives.
The thermoelectric figure of merit “ZT” describes the suitability of thermoelectric materials and is defined as follows:
Equation 1
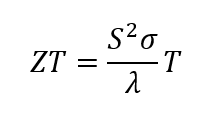
Thermoelectric materials should have low thermal conductivity and high electrical conductivity in addition to a Seebeck coefficient that is as large as possible. Materials of high thermal conductivity do not allow large temperature gradients; if electrical conductivity is low, no useful currents can be obtained.
Moreover, the figure of merit and temperature difference are directly related to the efficiency η of a thermoelectric device, so this increases when ZT and ΔT have large values.
Equation 2
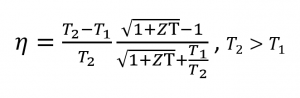
Optimization of thermoelectric materials
A wide variety of material classes exhibit thermoelectric effects of different strengths. For a long time, a value of 1 was considered the maximum figure of merit, but today some optimized materials achieve values of around 2 or higher.
As can be seen from equation 1, there are two different approaches to increase ZT: either the power factor S2σ can be maximized, and/or the thermal conductivity can be minimized. To achieve this, existing materials are improved, e.g. by doping, and new materials are developed. The latter can be achieved, for example, by nanostructuring, since this greatly reduces the thermal conductivity without greatly influencing the power factor. If thermoelectrics are used in industry, cost, toxicity and availability of materials are key considerations.
Measurement of the figure of merit
Various methods are available for determining the thermoelectric figure of merit.
- First, the individual parameters (Seebeck coefficient, electrical and thermal conductivity) can be measured, and ZT calculated according to equation 1.
- On the other hand, it is possible to determine ZT directly using the Harman method.
1. Calculation of equation 1
Various commercial devices are available for quasi-simultaneous measurement of the electrical conductivity and the Seebeck coefficient. Thermal conductivity is usually determined by the laser or light flash method. The direct result of this method is the thermal diffusivity. If you know the density and specific heat capacity.
The thermal conductivity can be calculated therefrom by means of the following formula:
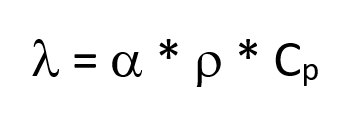
All these variables are temperature dependent
Therefore, a total of five (temperature-dependent) variables must be determined in order to calculate the figure of merit. An error analysis can be found in the literature [1].
2. Determinaton with harman method
The Harman method allows direct measurement of the figure of merit. This is achieved by passing a small current through a rod-shaped sample under adiabatic conditions. The observed voltage drop is composed of an ohmic (UR; electrical resistance) and a thermoelectric component caused by the Seebeck effect (Uth; thermal voltage). In contrast to the Ohmic component, which occurs spontaneously, the one caused by the Seebeck effect builds up slowly:
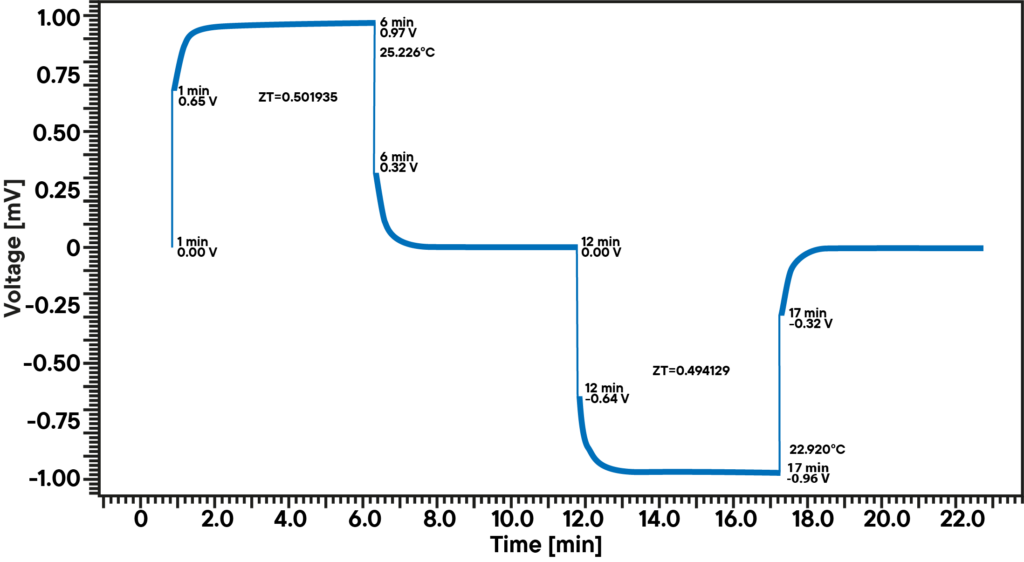
The figure of merit is obtained by dividing the two components:
Equation 4
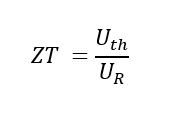
Literature:
[1] A. Alleno et al., A round robin test of the uncertainty on the measurement.of the thermoelectric dimensionless figure of merit of Co0.97Ni0.03Sb3, REVIEW OF SCIENTIFIC INSTRUMENTS 86, 011301 (2015).
[2] T.C. Harman, Journal of Applied Physics 29, 1373 (1958).
[3] T. C. Harman, J. H. Cahn, and M. J. Logan, J. Appl. Phys. 30(9), 1351 (1959).
