Thermischer Kontaktwiderstand

Was ist der thermische Kontaktwiderstand?

Der thermische Kontaktwiderstand kennzeichnet die Übertragung der Wärme an der Grenzfläche zwischen zwei Festkörpern.

Aufgrund der Herstellungs- und Bearbeitungsprozesse, aber auch dessen intrinsischen Materialeigenschaft sind Rauheiten an der Oberfläche unvermeidlich. Infolgedessen ist nicht die gesamte Fläche der beiden Festkörper in direkten Kontakt, sondern nur ein Bruchteil und dementsprechend nicht am Wärmetransport beteiligt.

Die entstehenden Hohlräume zwischen den Festkörpern sind üblicherweise mit Luft, einem schlechten Wärmeleiter, gefüllt. [1,2] Ein Temperatursprung an der Grenzfläche ist die Folge.

Für den spezifischen thermischen Kontaktwiderstand gilt:[1]

mit
rK: spezifischer thermischer Kontaktwiderstand in (m²K)/W
A: nominale (makroskopische) Kontaktfläche ohne Rauheit in m²
Q ̇: Wärmestrom durch die Kontaktfläche A in W
ΔT: Temperatursprung an der Kontaktfläche A in K.

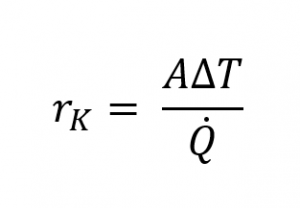
Dessen Kehrwert wird auch als thermischer Kontaktkoeffizient bezeichnet. Der Quotient aus spezifischen thermischen Kontaktwiderstand rk und der makroskopischen Kontaktfläche A wird als thermischer Kontaktwiderstand bezeichnet:

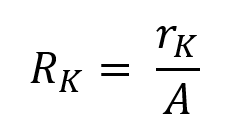
Die Einheit des thermischen Kontaktwiderstandes ist (K/W).

Durch was kann der thermische Kontaktwiderstand beeinflusst werden?

• Oberflächenrauigkeit der Festkörper
• Anpressdruck auf die Kontaktfläche zwischen den zwei Festkörpern
• Füllen der Hohlräume zwischen den Kontaktflächen durch besser wärmleitende Materialien, wie zum Beispiel: Gele, Pasten, Phase-Change Materialien, Folien, Klebestoffe, thermische Interfacematerialien etc.
• Im Allgemeinen bestimmt die Kombination der beiden Festkörper den thermischen Kontaktwiderstand

Ein stark vereinfachtest Modell zur Berechnung des thermischen Kontaktwiderstandes lässt sich anhand eines Widerstandsmodells aufstellen. Der Wärmefluss wird in Festkörper- und Fluidanteil aufgespalten und gesondert behandelt. Im Festkörperpfad befinden sich zwei in Serie geschaltete Widerstände. Der Anteil durch das Fluid wird durch die eingeschlossene Luft gebildet. Der Wärmetransport erfolgt parallel über beide Kanäle, weshalb sich diese im Ersatzschaltbild als Parallelschaltung darstellen lässt. (vgl. Abbildung 1)

Mithilfe des Ersatzschaltbildes und den bekannten Regeln für die Berechnung des Widerstandes in Serien- und Parallelschaltung ergibt sich folgende Formel [1]:

mit

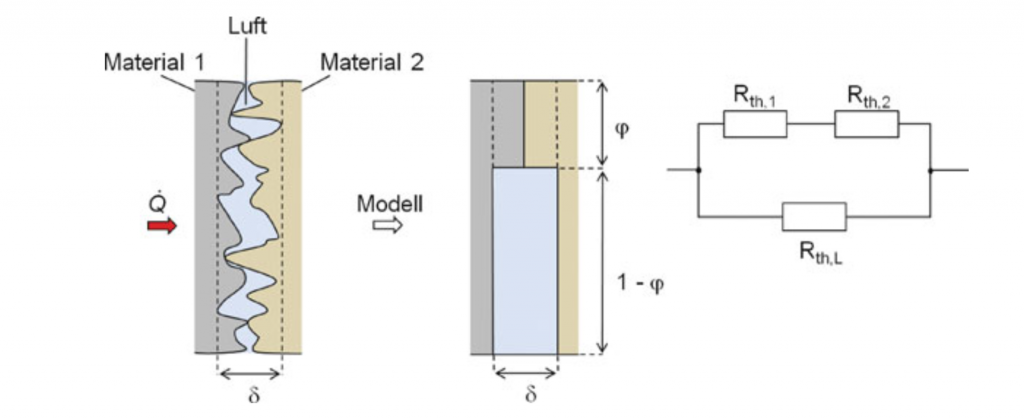
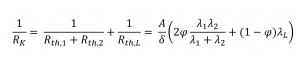
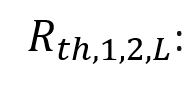
Thermischer Widerstand der Materialien 1,2 bzw. der Luft in K/W
Es gilt:

δ: Dicke der Grenzschicht in m
λ_(1,2,L): Wärmeleitfähigkeit der Materialien 1, 2, bzw. des Materials im Spalt (im Allgemeinen Luft) in W/(m K)
A: nominale (makroskopische) Kontaktfläche ohne Rauheit in m^2
φ: Anteil der Feststoff-Kontaktfläche an der nominalen Fläche A

Das Modell besitzt einige Schwachstellen. Zum einen beachtet es in keinster Weise die Wärmeübertragung in Form von Strahlung und zum anderen ist die Grenzschichtdicke δ und der Teil der nominalen Fläche der an der Wärmeübertragung teilnimmt φ nur in den seltensten Fällen bekannt.

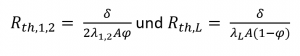
Wie messe ich den thermischen Kontaktwiderstand?

Der thermische Kontaktwiderstand kann zum Beispiel mit Hilfe eines „Thermal Interface Material Tester“ (TIM-Tester) ermittelt werden. Misst man mit einem TIM-Tester die thermische Impedanz eines Materials für verschiedene Dicken in dem ein Wärmestrom durch die Probe hindurch angelegt wird.

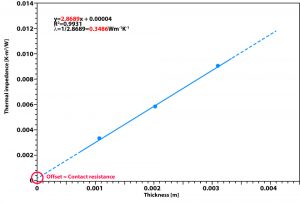
Aus den Messpunkten kann mittels linearer Regression eine steigende Gerade und aus deren Steigung die Wärmeleitfähigkeit ermittelt werden. Der Achsenabschnitt der Geraden entspricht dem thermischen Kontaktwiderstand zwischen dem Material und dem Messblock. Der Messblock kann beispielsweise aus Messing oder einer Kupfer- oder Aluminiumlegierung hergestellt sein.

Ein Beispiel für eine solche Messung ist in Abbildung 2 dargestellt. Es handelt sich hierbei um eine Messung der thermischen Impedanz von einer VespelTM-Probe mit einer Größe von 25 mm x 25 mm und einem angelegten Kontaktdruck von 1 MPa.

Im Beispiel wurden Proben mit einer Dicke zwischen 1,1 mm und 3,08 mm vermessen.

Literatur:

[1] Griesinger, Andreas. Wärmemanagement in der Elektronik, Springer Berlin Heidelberg, 2019.

[2] Incropera, DeWitt, Bergmann, Lavine, Fundamentals of heat and mass transfer.pdf“,  John Wiley & Sons, 2017.