Beschreibung
Auf den Punkt gebracht
Mit der Linseis LSR-Plattform können thermoelektrische Materialien in Form von Bulk-Materialien und dünnen Schichten auf einfache und komfortable Weise charakterisiert werden. In der Basisversion – LSR-1 – können sowohl der Seebeck-Koeffizient als auch der elektrische Widerstand vollautomatisch und gleichzeitig von -160°C bis 200°C gemessen werden.
Die Basisversion des LSR-1 (RT bis 200°C) kann mit verschiedenen Optionen kombiniert werden, um den Anwendungsbereich zu erweitern. So ermöglicht die Tieftemperatur-Option vollautomatische Messungen mit LN2-Kühlung bis -160°C sowie Quenchkühlung bis 80 K (nur Widerstand). Eine optionale Hochtemperatur-Sonde ermöglicht Widerstandsmessungen bis zu 600°C.
Das LSR-1 System ermöglicht die Charakterisierung von metallischen und halbleitenden Proben nach der bekannten Van-der-Pauw- (Widerstand) sowie der statischen Gleichstrom- und Steilheits-Seebeck-Koeffizienten-Messtechnik.
Der kompakte Tischaufbau ermöglicht einen vollautomatischen und softwaregesteuerten Betrieb. Die umfangreiche Windows-basierte Software bietet eine einfach zu bedienende Benutzeroberfläche, einschließlich Assistenten zur Erstellung eines Messprofils, Rückmeldungen zur Zuverlässigkeit der Messdaten und eine integrierte Messdatenauswertung und -speicherung. Die vakuumdichte Messkammer in Kombination mit einer Auswahl an Gasdosiersystemen stellt sicher, dass alle Anwendungsbereiche abgedeckt werden können.
Prinzip der Messung des Seebeck-Koeffizienten
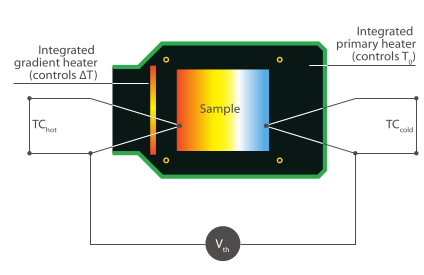
- Die Probentemperatur sowie der Temperaturgradient werden durch eine im Probenhalter eingebettete Heizung gesteuert.
- Die Probentemperatur kann auf ca. -160°C heruntergekühlt werden. Somit kann der spezifische Widerstand bis zu einer niedrigsten Temperatur von -160°C gemessen werden.
- Die Messung des Seebeck-Koeffizienten ist bis zu einer mittleren Probentemperatur von + 180°C möglich.
- Erhöhte Präzision bei der Temperaturmessung: Die einzelnen TC-Drähte berühren die Probenoberfläche orthogonal zur Richtung des Temperaturgradienten. Beide Kontaktpunkte haben die gleiche Temperatur. Mit dieser Methode wird die Oberflächentemperatur der Probe gemessen und nicht die Temperatur einer auf die Probenoberfläche gepressten TC-Perle. Auf diese Weise ist es auch unerheblich, ob die Temperatur der Probenoberfläche durch die TC-Drähte beeinflusst wird, die Wärme von/zu der Probe übertragen.
- Verbesserte Präzisions-Thermospannungsmessung: Die Seebeck-Spannung wird zwischen den beiden negativen TC-Drähten gemessen, was die genaueste räumliche Zuordnung zwischen Temperatur- und Thermospannungsmessung ermöglicht. So tritt die Seebeck-Spannung genau an den Stellen auf, an denen auch die Temperatur gemessen wird.
- Die Seebeck-Spannung wird zusammen mit dem Temperaturgradienten aufgezeichnet, während die Leistung des Gradientenheizers linear erhöht wird. Die Dauer eines einzelnen Messdurchlaufs beträgt etwa 30 bis 90 Sekunden, einschließlich der Hochgeschwindigkeits-Abtastrate. Die Werte werden einmal pro Sekunde abgetastet.
- Die Steigung der Thermospannung über Delta T wird mit einer linearen polynomialen Regression angepasst. Dank dieser dynamischen Auswertemethode können auftretende Offsets bei der Temperaturgradientenmessung vernachlässigt werden und die Messgenauigkeit wird erhöht. Aufgrund der kurzen Dauer der eigentlichen Messung haben Offset-Drifts einen sehr geringen Einfluss auf das Ergebnis.
Prinzip der Widerstandsmessung
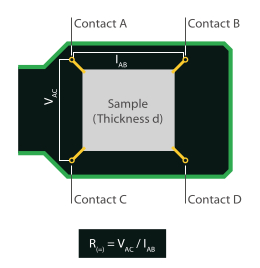
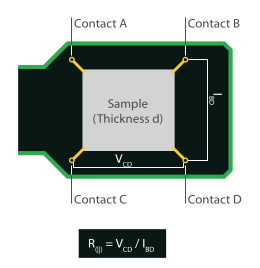
Zur Bestimmung des spezifischen elektrischen Widerstands (oder der elektrischen Leitfähigkeit) der Probe wird die Van-der-Pauw-Messtechnik verwendet. Dadurch können beliebig geformte Proben analysiert werden, störende Einflüsse wie Kontakt- oder Drahtwiderstände werden unterdrückt und die Messgenauigkeit kann deutlich erhöht werden.
Für die Van-der-Pauw-Messung muss die Probe mit vier Elektroden direkt an der Kante verbunden werden. Im ersten Schritt des Routings wird an zwei Kontakten an einer Kante der Probe ein Strom zum Fließen gebracht und die Spannung an den beiden anderen Kontakten an der gegenüberliegenden Kante gemessen. Aus diesen beiden Werten lässt sich mit Hilfe des Ohmschen Gesetzes ein Widerstand ermitteln. Im zweiten Schritt werden die Kontakte zyklisch geschaltet, und die Messung wird wiederholt. Der Schichtwiderstand der Probe kann dann leicht berechnet werden, indem die beiden gemessenen Widerstände (horizontal und vertikal) in die Van-der-Pauw-Formel eingesetzt und gelöst werden.
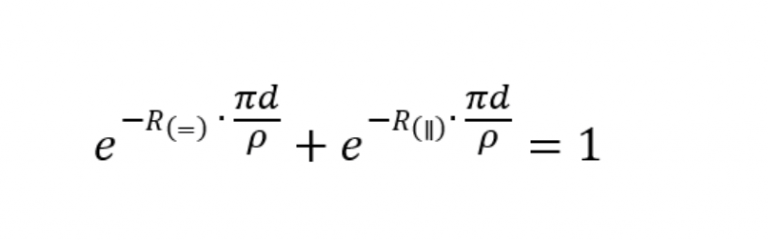
Ausgehend von den gemessenen Daten und dem Thermoelementabstand “t” können der spezifische Widerstand und die elektrische Leitfähigkeit nach folgenden Formeln berechnet werden:
Unique Features

Modulares Systemdesign,
aufrüstbar mit Gasspülsystem,
Beleuchtung und Kryo-Option.
Vakuumdichte Messkammer für
Messungen unter
definierten Atmosphären.
Austauschbare Probenträger mit
integrierter Primär- und Sekundärheizung
und einfachem Kontaktmechanismus.
Simultane Messung des Seebeck-Koeffizienten und des
elektrischen Widerstands (Widerstandsfähigkeit).
Vollautomatische, softwaregesteuerte
Messungen mit Exportmöglichkeiten der
Rohdaten in verschiedene Formate.
Fragen? Rufen Sie uns einfach an!
+49 (0) 9287/880 0
Donnerstag von 8-16 Uhr erreichbar
und Freitag von 8-12 Uhr.
Wir sind für Sie da!
Spezifikationen
Schwarz auf Weiß

Besondere Merkmale
- Modulares Systemdesign. Kann mit Gasspülsystem, Beleuchtung und Kryo-Option aufgerüstet werden.
- Vakuumdichte Messkammer für Messungen unter definierten Atmosphären.
- Einfach zu bedienende und austauschbare Probenträger mit integrierter Primär- und Sekundärheizung.
- Integrierte hochmoderne Messtechnik für genaueste Ergebnisse bei anspruchsvollen Proben.
- Die Einheit kann zur simultanen Messung sowohl des Seebeck-Koeffizienten als auch des elektrischen Widerstands (Widerstandsfähigkeit) verwendet werden.
- Der Probenträger verwendet einen speziellen Kontaktmechanismus für einfache Probenvorbereitung und ermöglicht Messungen mit hoher Reproduzierbarkeit.
- V-I-Kennlinienmessung kann durchgeführt werden, um festzustellen, ob der Sensor guten Kontakt mit der Probe hat.
- Das System ermöglicht vollautomatische, softwaregesteuerte Messungen mit vordefinierten Temperatur- und Messprofilen.
- Die gemessenen Rohdaten werden auf der Festplatte gespeichert und können in mehreren Datenformaten zur Weiterverarbeitung in Microsoft Excel oder Origin exportiert werden.
- Das System wird mit Constantan-Referenz inklusive Tabellen und Zertifikat geliefert.
MODELL | LSR-1 |
|---|---|
| Temperaturbereich: | Grundeinheit: RT bis 200°C Option Kryo: -160°C bis +200°C |
| Grundsätze der Messung: | Seebeck-Koeffizient Messbereich: 0 bis 2,5 mV/K – Temperaturgradient bis zu 10K Seebeck-Spannungsmessung: Bereich +-8 mV |
| Atmosphären: | Inert, reduzierend, oxidierend, Vakuum Heliumgas mit niedrigem Druck, empfohlen |
| Probenhalter: | Integrierte PCB-Platine mit Primär- und Sekundär-Heizung |
| Probenumfang (Seebeck): | L: 8 mm bis 25 mm; B: 2 mm bis 25 mm; T: Dünnfilm bis 2 mm |
| Probengröße (Widerstandsfähigkeit): | L: 18 mm bis 25 mm; B: 18 mm bis 25 mm; T: dünne Folie bis 2 mm |
| Vakuumpumpe: | optional |
| Heizrate: | 0.01 – 100 K/min |
| Temperaturgenauigkeit: | ±1,5 °C oder 0,0040 ∙ | t | |
| Elektrischer Widerstand: | 10 nOhm |
| Thermospannung: | 0.5 nV/K (nV = 10-9 V) |
Datenblatt
Software
Werte sichtbar und vergleichbar machen
Die leistungsfähige, auf Microsoft® Windows® basierende LINSEIS Thermoanalyse-Software übernimmt neben der verwendeten Hardware die wichtigste Funktion bei der Vorbereitung, Durchführung und Auswertung von thermoanalytischen Experimenten. Mit diesem Softwarepaket bietet Linseis eine umfassende Lösung für die Programmierung aller gerätespezifischen Einstellungen und Steuerfunktionen sowie für die Datenspeicherung und -auswertung. Das Paket wurde von unseren hauseigenen Softwarespezialisten und Applikationsexperten entwickelt und hat sich seit Jahren bewährt.
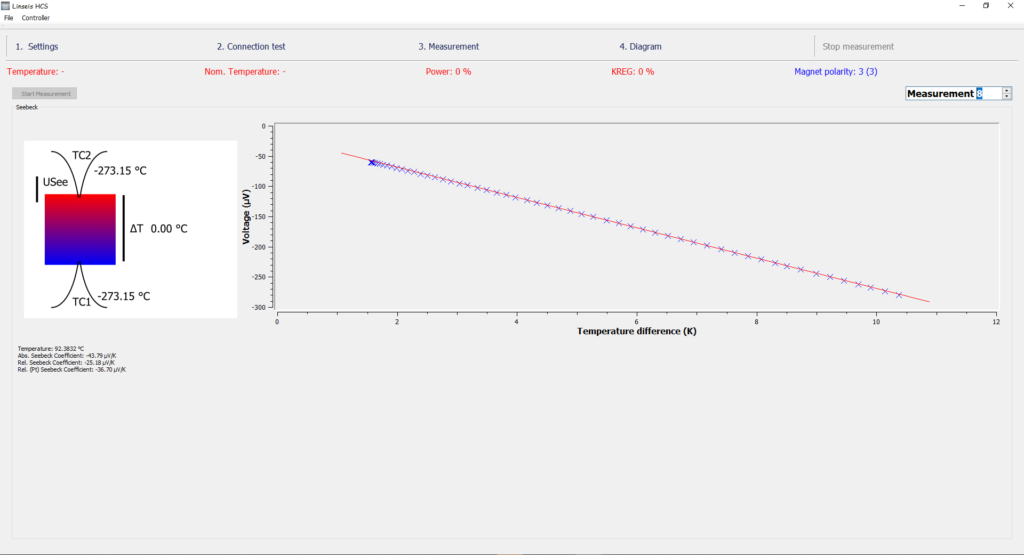
Allgemeine Eigenschaften
- Automatische Auswertung des Seebeck-Koeffizienten und der elektrischen Leitfähigkeit
- Automatische Kontrolle der Probenkontaktierung
- Erstellung von automatische Messprogrammen
- Erstellung von Temperaturprofilen und Temperaturgradienten für die Seebeck-Messung
- Farbwiedergabe in Echtzeit
- Automatische und manuelle Skalierung
- Frei wählbare Darstellung der Achsen(z.B. Temperatur (x-Achse) versus Delta L (y-Achse))
- Mathematische Berechnungen (z. B. erste und zweite Ableitung)
- Datenbank zur Archivierung aller Messungen und Auswertungen
- Multitasking (verschiedene Programme können gleichzeitig verwendet werden)
- Multi-User-Option (Benutzerkonten)
- Zoom-Optionen für Kurvenschnitte
- Eine beliebige Anzahl von Kurven kann zum Vergleich übereinander geladen werden
- Menü-Online-Hilfe
- Freie Beschriftung von Kurven
- Vereinfachte Exportfunktionen (CTRL C)
- EXCEL®- und ASCII-Export von Messdaten
- Statistische Trendauswertung (Mittelwertkurve mit Konfidenzintervall)
- Tabellarische Darstellung der Daten
Applikationen
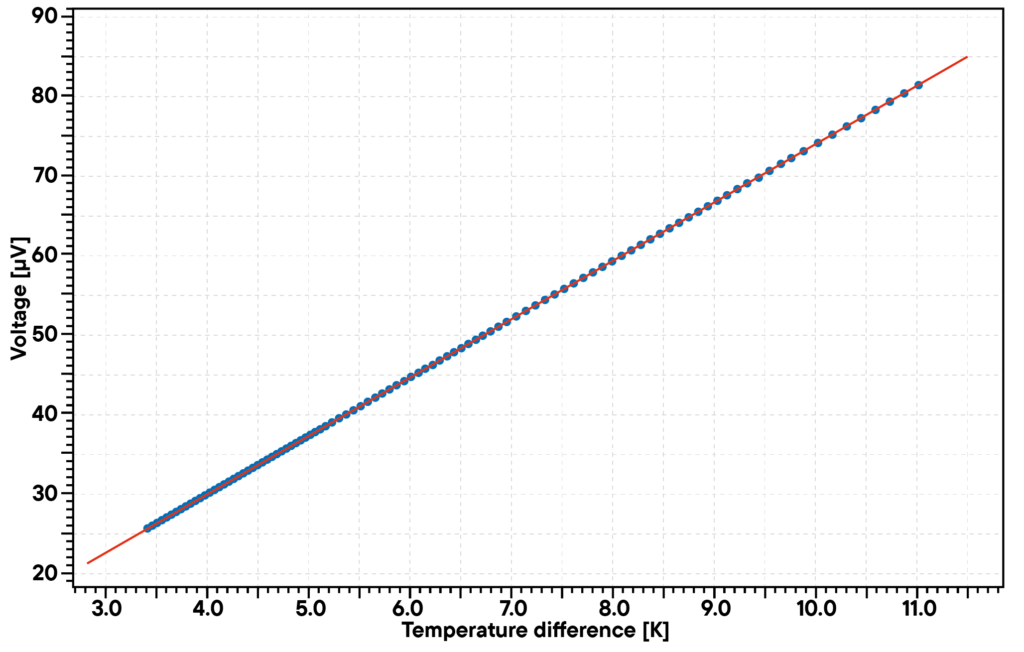
Anwendungsbeispiel: Auswertung gewonnener Daten durch lineare Regression
Seebeck-Spannung/Temperaturgradient (blau), gemessen während des Sweeps der Gradientenheizungsleistung zusammen mit der linearen Regression (rot). Der Seebeck-Koeffizient wird durch die Steigung der linearen Regression bestimmt.
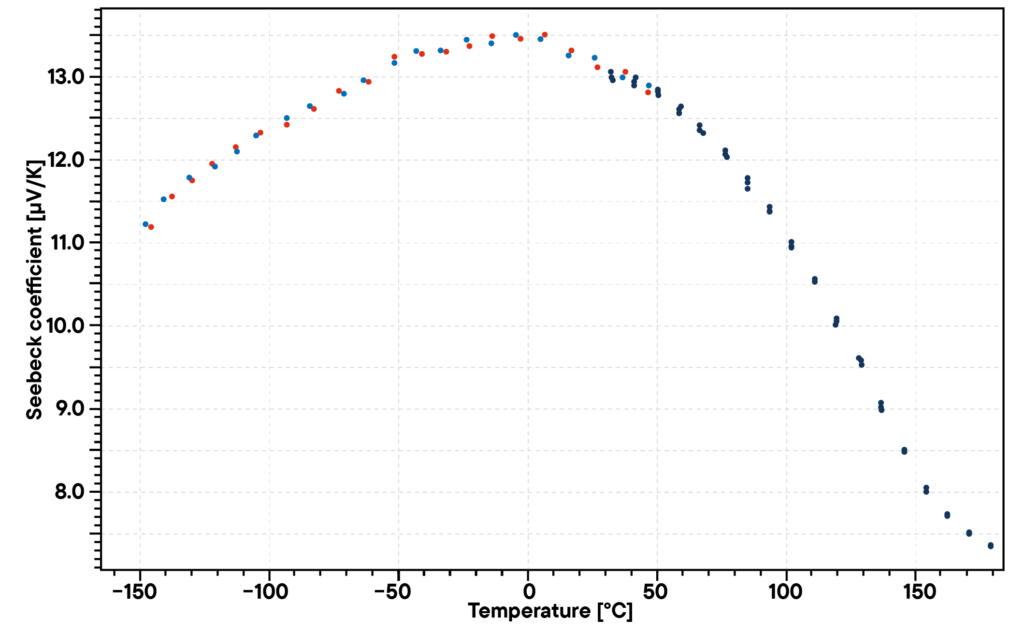
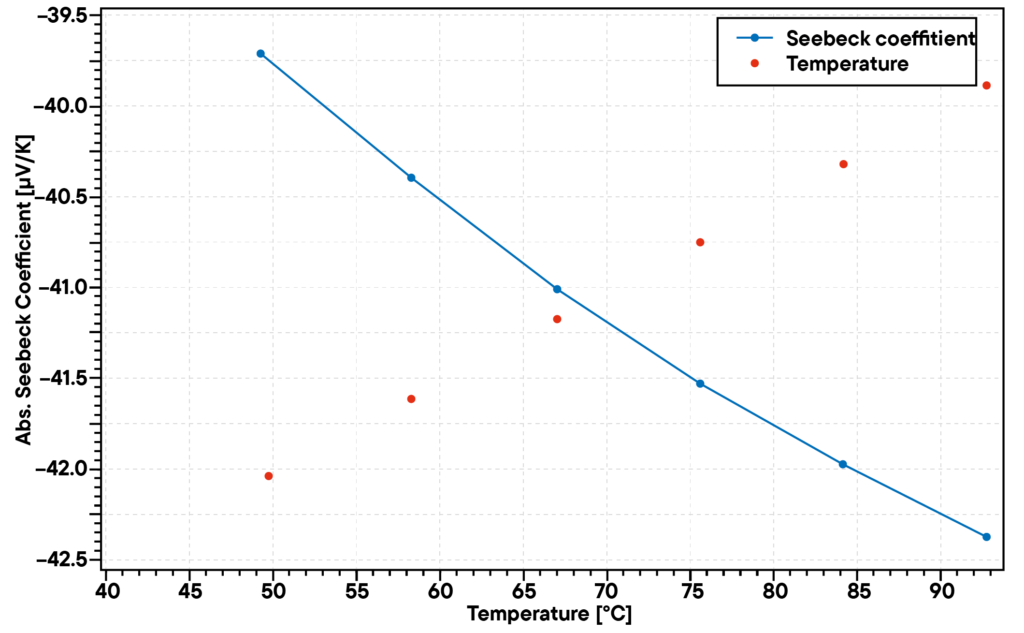
Anwendungsbeispiel: Datenauswertung
Bei dieser Methode wird der Seebeck-Koeffizient relativ zu Alumel gemessen. Um den absoluten Seebeck-Koeffizienten zu berechnen, wird Platin relativ zum Alumel-Draht über die Temperatur gemessen.
Anwendungsbeispiel: Seebeck-Koeffizient im Vergleich zur Temperatur
Beispiel für die Messung des Seebeck-Koeffizienten von Konstantan.
Videos
Bestens informiert



