Linseis > Conhecimentos > Análise de materiais termoeléctricos – a figura de mérito e a sua medição

Análise de materiais termoeléctricos – a figura de mérito e a sua medição

O que são materiais termoeléctricos?

Os materiais termoeléctricos podem converter o calor diretamente em energia eléctrica. Esta propriedade baseia-se no efeito Seebeck em que uma diferença de temperatura aplicada a um material gera uma tensão. O inverso é o efeito Peltier, que é normalmente utilizado para arrefecimento. Um terceiro efeito termoelétrico é o efeito Thomson, que descreve o transporte de calor ao longo de um condutor de corrente no qual existe um gradiente de temperatura.

Devido à possibilidade de utilizar diretamente a energia térmica, os materiais termoeléctricos tornaram-se o foco da investigação e desenvolvimento. Por um lado, podem ser utilizados para gerar energia eléctrica a partir de fontes de energia primária; por outro lado, é tentador gerar eletricidade a partir de calor residual, conservando assim os recursos de combustíveis fósseis e, ao mesmo tempo, minimizando o consumo de energia. libertação de CO2 .

Uma vez que a tensão eléctrica induzida pelo efeito Seebeck é muito baixa (normalmente entre algumas e algumas centenas de μV/K), estão a ser feitos grandes esforços para desenvolver materiais termoeléctricos melhorados.

Os materiais termoeléctricos clássicos provêm do grupo dos semimetais e dos semicondutores (IV a VI grupo principal do PSE) ou são ligas de materiais destes grupos, uma vez que o coeficiente Seebeck é particularmente elevado. O efeito Seebeck pode ainda ser aumentado por dopagem.

Qual é o número de qualidade?

Em geral, um valor de mérito é uma medida da adequação de materiais, métodos ou dispositivos em comparação com alternativas.

O valor de mérito termoelétrico ZT ( figura de mérito “) descreve a adequação dos materiais termoeléctricos e é definido da seguinte forma:

Equação 1

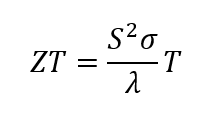
Para além do coeficiente de Seebeck mais elevado possível, os materiais termoeléctricos devem ter uma baixa condutividade térmica e uma elevada condutividade eléctrica elevada. Os materiais com elevada condutividade térmica não permitem grandes gradientes de temperatura; se a condutividade eléctrica for baixa, não é possível obter correntes utilizáveis.

Além disso, a figura de mérito e a diferença de temperatura estão diretamente relacionadas com a eficiência η de uma unidade termoeléctrica, pelo que esta aumenta quando ZT e ΔT têm valores elevados

Equação 2

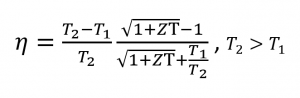
Otimização de materiais termoeléctricos

Uma grande variedade de classes de materiais apresenta efeitos termoeléctricos de diferentes intensidades. Durante muito tempo, um valor de 1 foi considerado como o valor máximo de mérito, mas atualmente alguns materiais optimizados atingem valores de 2 ou superiores.

Como se pode ver na equação 1, há duas abordagens diferentes para aumentar o ZT: ou o chamado fator de potência S2σ pode ser maximizado e/ou a condutividade térmica pode ser minimizada. Para o conseguir, os materiais existentes são melhorados, por exemplo, por dopagem, e são desenvolvidos novos materiais. Este último pode ser conseguido através da nanoestruturação, por exemplo, uma vez que reduz consideravelmente a condutividade térmica sem afetar significativamente o fator de potência. Se a termoeletricidade for utilizada na indústria, os custos, a toxicidade e a disponibilidade dos materiais são importantes.

Medição do valor de mérito

Existem vários métodos para determinar a figura de mérito termoelétrico.

Por um lado, os parâmetros individuais (coeficiente de Seebeck, condutividade eléctrica e térmica) podem ser medidos e a ZT calculada de acordo com a equação 1.
Por outro lado, é possível utilizar a ZT diretamente através do chamado método Harman método.

1. cálculo de acordo com a equação 1

Existem vários dispositivos comerciais estão disponíveis para a medição quase simultânea da condutividade eléctrica e do coeficiente de Seebeck. A condutividade térmica ou difusividade térmica é normalmente determinada utilizando o método do laser ou do flash de luz. O resultado direto deste método é a difusividade térmica. Se a densidade e a condutividade térmica específica forem conhecidas.

A condutividade térmica pode ser calculada a partir da seguinte fórmula?

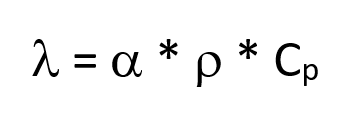
Todas estas variáveis dependem da temperatura.

Isto significa que um total de cinco variáveis (dependentes da temperatura) devem ser determinadas para calcular a figura de mérito. Uma análise de erro pode ser encontrada na literatura [1].

2. determinação pelo método de Harman

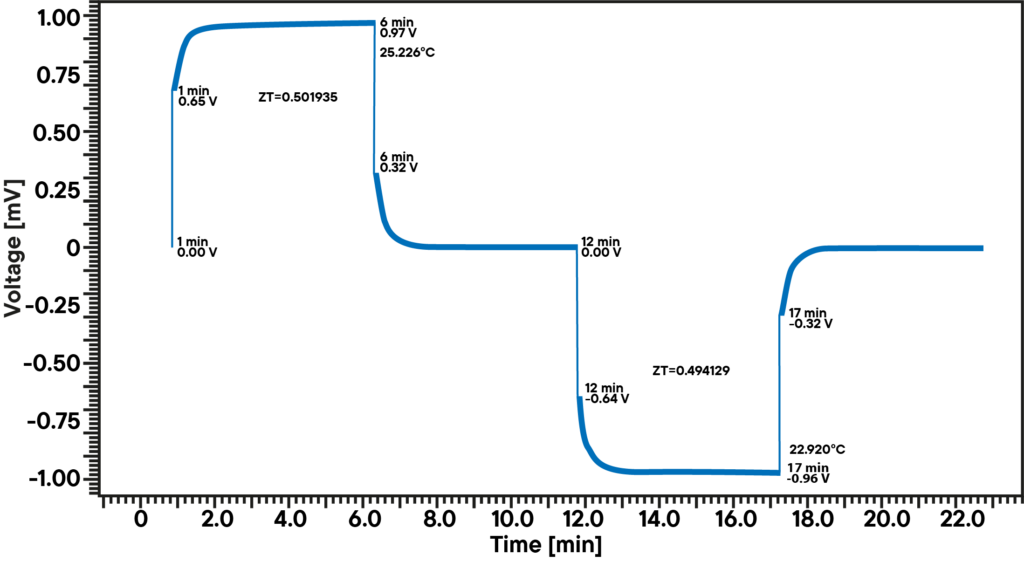
O chamado método Harman permite a medição direta da figura de mérito. Para o efeito, faz-se passar uma pequena corrente através de uma amostra em forma de barra em condições adiabáticas. A queda de tensão observada é composta por um componente óhmico (UR; resistência eléctrica) e um componente termoelétrico causado pelo efeito Seebeck (Uth; tensão termoeléctrica). Ao contrário da componente óhmica, que ocorre espontaneamente, a componente causada pelo efeito Seebeck acumula-se lentamente:

O número de qualidade obtém-se dividindo as duas proporções:

Equação 4

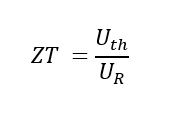
Literatura:

[1] A. Alleno et al, A round robin test of the uncertainty on the measurement.of the thermoelectric dimensionless figure of merit of Co0.97Ni0.03Sb3, REVIEW OF SCIENTIFIC INSTRUMENTS 86, 011301 (2015).

[2] T.C. Harman, Journal of Applied Physics 29, 1373 (1958).

[3] T. C. Harman, J. H. Cahn, e M. J. Logan, J. Appl. Phys. 30(9), 1351 (1959).

Gostaste do artigo ?

Ou ainda tens dúvidas? Não hesites em entrar em contacto!

+49 9287 / 880 - 0

Katharina

+49 9287 / 880 - 0

+49 9287 / 880 – 0

[email protected]

Artigos que também poderás gostar

Laser Flash Analyzer: Caracterização térmica moderna de materiais de isolamento na indústria da construção

Com as crescentes exigências de eficiência energética e sustentabilidade, a caraterização exacta das propriedades térmicas dos materiais de isolamento está a ganhar destaque. A condutividade térmica (λ) é o parâmetro-chave para avaliar o desempenho do isolamento – tanto quando novo como ao longo de todo o ciclo de vida de um material de construção.

Ligas refractárias (ligas refractárias): Produção e aplicação em ambientes extremos

As ligas refractárias feitas de materiais como o tungsténio, o molibdénio, o nióbio, o tântalo, o rénio e o vanádio desempenham um papel fundamental em aplicações extremas na indústria aeroespacial, na tecnologia nuclear, na indústria de alta temperatura, na tecnologia médica e na eletrónica

Diferença de dilatação térmica em juntas coladas: Desafios e soluções para juntas coladas fiáveis

Nos modernos conceitos de design para a indústria automóvel, aeroespacial e eletrónica, as montagens híbridas feitas de vários materiais leves, como o alumínio, o aço e os plásticos reforçados com fibras de carbono (CFRP), são cada vez mais unidas utilizando a tecnologia de ligação adesiva.

Como a Análise Térmica Ajuda a Prever e Reduzir o Desprendimento de Microfibras dos Têxteis

Nos conceitos de design modernos para a indústria automóvel, aeroespacial e eletrónica, as montagens híbridas feitas de vários materiais leves, como o alumínio, o aço e os plásticos reforçados com fibra de carbono (CFRP), são cada vez mais unidas utilizando a tecnologia de ligação adesiva.

Análise termomecânica de metais – Caracterização fiável de materiais para aço e ligas

As empresas da indústria do aço e do metal são confrontadas com exigências cada vez maiores: Os componentes têm de suportar cargas térmicas elevadas, as janelas de processo têm de ser cumpridas com precisão e as alterações microestruturais direcionadas são frequentemente a chave para melhorar as propriedades dos materiais.

Cinética avançada e análise do processo de redução de hidrogénio do minério de ferro com os sistemas TGA e STA da Linseis

A redução direta do minério de ferro com hidrogénio é central para a descarbonização da indústria siderúrgica. Os processos baseados em hidrogénio permitem uma redução significativa das emissões de CO₂ em comparação com a redução convencional com transportadores de carbono.

Deteção de erros através da análise térmica: como o DSC melhora os protótipos funcionais no fabrico de aditivos

O fabrico aditivo estabeleceu-se como uma tecnologia transformadora na produção industrial – particularmente no desenvolvimento de protótipos funcionais.

Policarbonato: transparência e resistência ao impacto em aplicações técnicas

O policarbonato (PC) é um dos termoplásticos de engenharia mais importantes na moderna tecnologia de materiais. A sua combinação única de elevada transparência, resistência ao impacto pronunciada e excelente estabilidade térmica torna-o um material indispensável em numerosos sectores industriais.

Avalia a estabilidade das proteínas: Estratégias Analíticas para a Investigação Biomolecular

Compreender a estabilidade das proteínas é fundamental para a bioquímica moderna, a investigação farmacêutica e a biotecnologia.