Indice dei contenuti
Cosa sono i materiali termoelettrici?
I materiali termoelettrici possono convertire il calore direttamente in energia elettrica. Questa proprietà si basa sull’effetto effetto Seebeck in cui una differenza di temperatura applicata a un materiale genera una tensione. L’effetto inverso è l’effetto Peltier, solitamente utilizzato per il raffreddamento. Un terzo effetto termoelettrico è l’effetto Thomson, che descrive il trasporto di calore lungo un conduttore che trasporta corrente in presenza di un gradiente di temperatura.
I materiali termoelettrici sono diventati oggetto di ricerca e sviluppo grazie alla loro capacità di utilizzare direttamente l’energia termica. Da un lato, possono essere utilizzati
Poiché la tensione elettrica indotta dall’effetto Seebeck è molto bassa (di solito da poche centinaia di μV/K), si stanno compiendo grandi sforzi per sviluppare materiali termoelettrici migliori.
I materiali termoelettrici classici appartengono al gruppo dei semimetalli e dei semiconduttori (dal IV al VI gruppo principale del PSE) o sono leghe di materiali di questi gruppi, in quanto il coefficiente di Seebeck è particolarmente elevato. L’effetto Seebeck può essere ulteriormente aumentato dal drogaggio.
Qual è il numero di qualità?
In generale, una cifra di merito è una misura dell’idoneità di materiali, metodi o dispositivi rispetto alle alternative.
La figura di merito termoelettrica ZT ( figura di merito “) descrive l’idoneità dei materiali termoelettrici ed è definita come segue:
Equazione 1
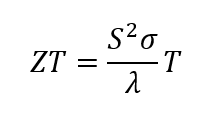
Oltre al più alto coefficiente di Seebeck possibile, i materiali termoelettrici dovrebbero avere una bassa conducibilità termica e un’alta conducibilità elettrica per quanto possibile. I materiali con un’elevata conducibilità termica non consentono grandi gradienti di temperatura; se la conducibilità elettrica è bassa, non è possibile ottenere correnti utilizzabili.
Inoltre, la figura di merito e la differenza di temperatura sono direttamente correlate all’efficienza η di un’unità termoelettrica, che aumenta quando ZT e ΔT hanno valori elevati.
Equazione 2
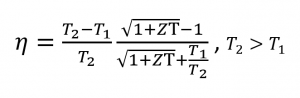
Ottimizzazione dei materiali termoelettrici
Un’ampia varietà di classi di materiali presenta effetti termoelettrici di diversa intensità. Per molto tempo, un valore di 1 è stato considerato come la cifra di merito massima, ma oggi alcuni materiali ottimizzati raggiungono valori di 2 o superiori.
Come si evince dall’equazione 1, esistono due approcci diversi per aumentare lo ZT: si può massimizzare il cosiddetto fattore di potenza S2σ e/o minimizzare la conduttività termica. Per raggiungere questo obiettivo, i materiali esistenti vengono migliorati, ad esempio tramite drogaggio, e ne vengono sviluppati di nuovi. Quest’ultimo può essere ottenuto, ad esempio, con la nanostrutturazione, che riduce notevolmente la conduttività termica senza incidere in modo significativo sul fattore di potenza. Se la termoelettrica viene utilizzata nell’industria, i costi, la tossicità e la disponibilità dei materiali sono importanti.
Misurazione della figura di merito
- Da un lato, i singoli parametri (coefficiente di Seebeck, conducibilità elettrica e termica) possono essere misurati e lo ZT può essere calcolato in base all’equazione 1.
- D’altra parte, è possibile utilizzare lo ZT direttamente con il cosiddetto metodo di metodo Harman metodo.
1. calcolo secondo l'equazione 1
Esistono diversi dispositivi commerciali sono disponibili per la misurazione quasi simultanea della conduttività elettrica e del coefficiente di Seebeck. La conducibilità termica o la diffusività termica vengono solitamente determinate con il metodo del laser o del flash di luce. Il risultato diretto di questo metodo è la diffusività termica. Se la densità e la conducibilità termica specifica sono note.
È possibile calcolare la conducibilità termica utilizzando la seguente formula?
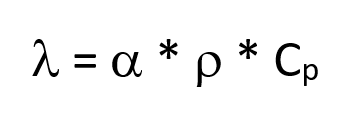
Tutte queste variabili dipendono dalla temperatura.
2. determinazione con il metodo Harman
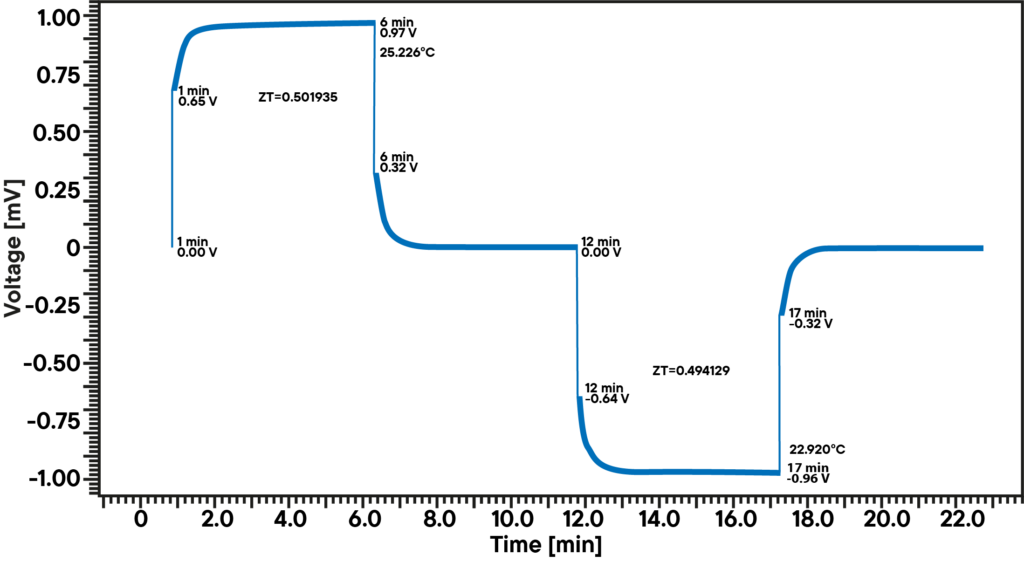
Equazione 4
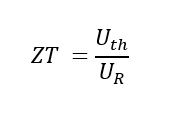
Letteratura:
[1] A. Alleno et al, A round robin test of the uncertainty on the measurement.of the thermoelectric dimensionless figure of merit of Co0.97Ni0.03Sb3, REVIEW OF SCIENTIFIC INSTRUMENTS 86, 011301 (2015).
[2] T.C. Harman, Journal of Applied Physics 29, 1373 (1958).
[3] T. C. Harman, J. H. Cahn e M. J. Logan, J. Appl. Phys. 30(9), 1351 (1959).