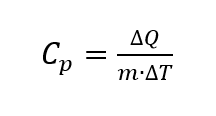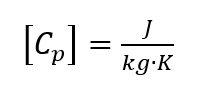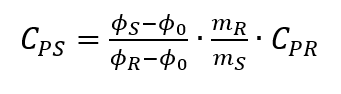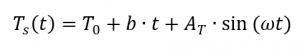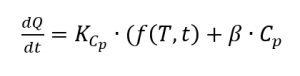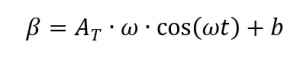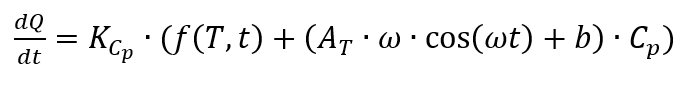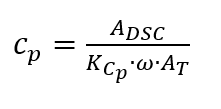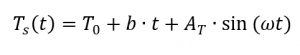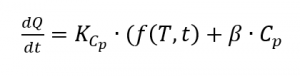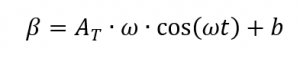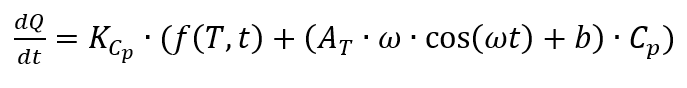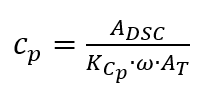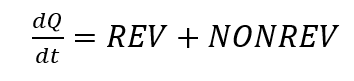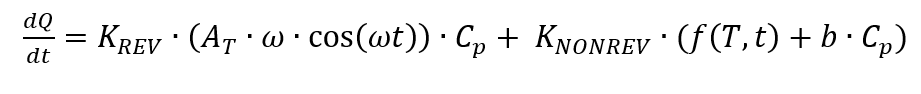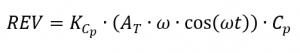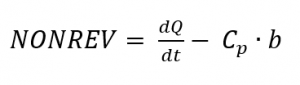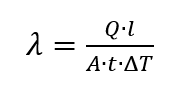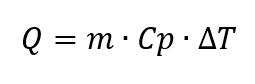“A capacidade térmica específica indica a capacidade de uma substância armazenar calor. Esta quantidade material corresponde à quantidade de calor necessária para aquecer uma certa quantidade de uma substância em um Kelvin.”
Os DSC podem ser utilizados para determinar a capacidade térmica específica (a seguir designada por Cp) [3, Cap. 6.2]. A capacidade térmica específica é uma quantidade intensiva adicionando a massa. Indica a quantidade de calor que uma substância deve absorver para aumentar a massa de uma substância por uma diferença de temperatura definida. A Cp é dependente da temperatura e é calculada de acordo com,
em que se assume que a pressão ambiente é constante [2, p. 118]. A unidade para a capacidade térmica específica [3, p. 78] é
Uma pressão constante, caracterizada pelo índice “p”, é um pré-requisito para medições DSC corretas. Além disso, a capacidade calorífica também pode ser representada assumindo um volume constante, que por sua vez é referido como Cv.
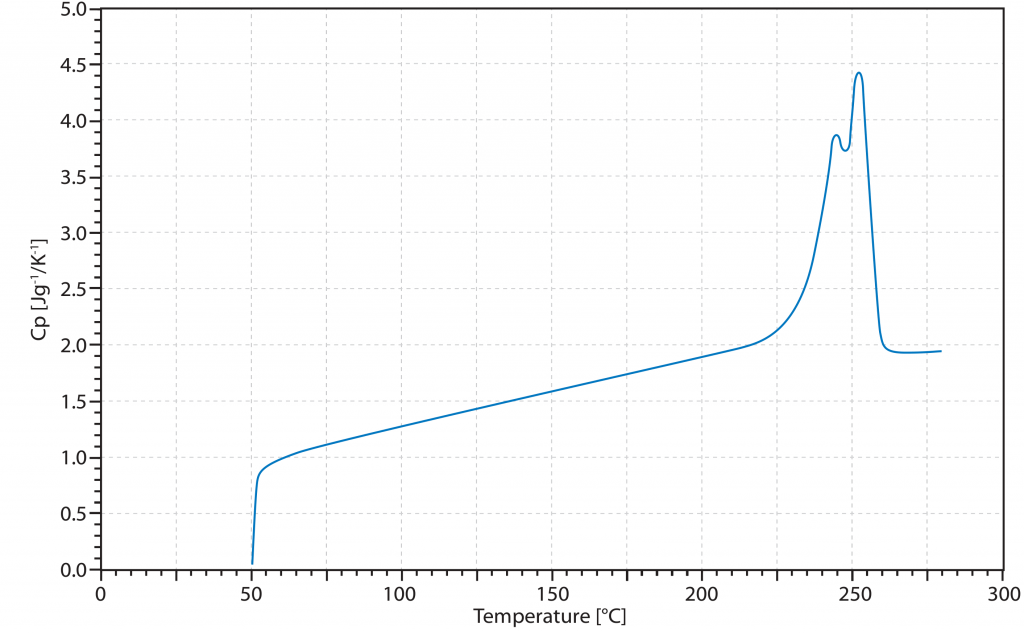
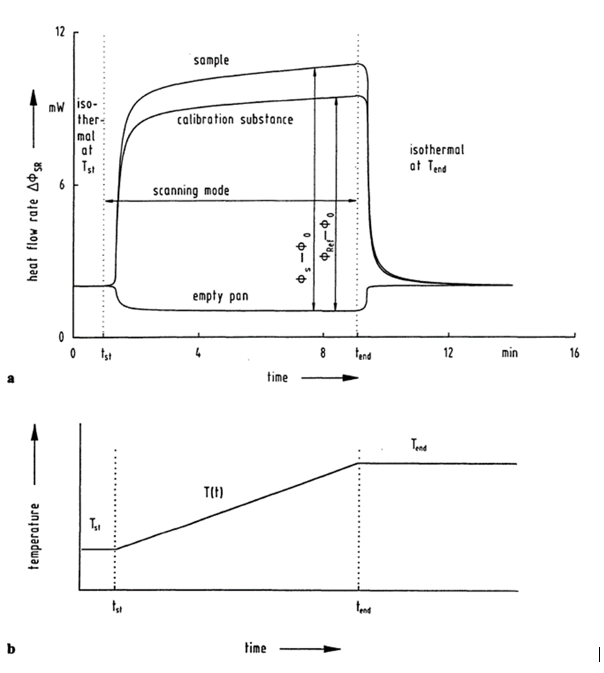
Abaixo (Fig. 1) encontra-se uma representação de uma curva CP típica de um sinal de medição DSC com um aumento supostamente significativo da capacidade calorífica específica no decurso de um processo de fusão.
A razão para o aumento do valor Cp apresentado é a natureza endotérmica desta transição. Isto significa que o sistema de medição tem de fornecer mais energia para seguir o perfil de temperatura especificado. No entanto, isto não corresponde ao Cp real e, por esta razão, a capacidade térmica específica na área de uma transição de fase é assumida como infinita.
Referenciar com a ajuda do Saphir
A safira é o padrão mais utilizado para a medição com DSC na determinação dos factores de correção para a medição da capacidade térmica específica. O cristal constituído por óxido de alumínio (a seguir designado por Al2O3 ) ocorre na forma natural. No entanto, a safira também pode ser produzida sinteticamente e com uma qualidade perfeita. Os vidros de safira produzidos sinteticamente são geralmente incolores e inertes devido à sua elevada temperatura de fusão de 2050 °C, na gama de temperaturas habitual dos DSC. A produção artificial permite que a safira seja fabricada com elevada precisão e representa um padrão muito exato. No entanto, as amostras com capacidades caloríficas específicas fortemente divergentes podem apresentar desvios de medição. Neste caso, deve ser utilizado um padrão com uma capacidade térmica específica comparável.
Métodos para determinar a capacidade térmica específica utilizando DSC
Existem vários métodos para determinar a capacidade térmica específica utilizando calorímetros diferenciais de varrimento. Apresenta-se de seguida uma breve descrição dos mesmos.
Medição clássica de CP utilizando DSC
A determinação clássica da capacidade térmica específica utilizando DSCs é efectuada em três etapas. Na primeira etapa, apenas o cadinho da amostra correspondente é aquecido e a curva zero correspondente ao ensaio é registada de modo a compensar a inércia do sistema de medição. Numa segunda fase, mede-se um material de referência conhecido nas mesmas condições de ensaio. O pré-requisito é que o material seja muito puro, bem definido e inerte na gama de temperaturas pretendida. Os valores da literatura para a capacidade térmica do material de referência em função da temperatura também devem estar disponíveis. Num terceiro passo, a amostra a ser analisada é medida sob as mesmas condições de ensaio. A curva zero é subtraída das medições da referência e da amostra. A partir da diferença entre as duas curvas DSC, um fator de calibração e a comparação dos fluxos de calor podem ser utilizados para calcular a capacidade térmica específica de acordo com
determina [4, p. 119]. A Fig. 2 apresenta uma ilustração das três curvas e do método.
Dado que são utilizados pesos de amostra muito pequenos, é necessário determinar com grande exatidão as massas do material de referência e da amostra. O cadinho e todas as outras condições ambientais devem ser mantidos tão idênticos quanto possível. Caso contrário, ocorrerão desvios de medição, devendo ser observado o posicionamento exato do cadinho e da amostra. O material de referência deve também ser semelhante à amostra a ensaiar em termos de peso e de capacidade térmica específica, a fim de minimizar influências como os gradientes de temperatura através da amostra.
Medição de CP com modulação de temperatura utilizando DSC
Ao determinar a capacidade térmica específica utilizando a medição com modulação de temperatura, uma onda sinusoidal é sobreposta à curva de temperatura. O pré-requisito para este método de medição é que o DSC possa seguir a temperatura modulada especificada. Por conseguinte, o perfil de temperatura [4, p. 132] pode ser descrito da seguinte forma:
Isto resulta no fluxo de calor de
com
[2, p. 187], o que significa que
Se a DSC medida for analisada, a capacidade térmica específica [1, p. 363] é calculada do seguinte modo
A inércia dos sistemas de medição e dos fornos limita a amplitude e exige longos períodos de duração. Para obter uma boa resolução da capacidade térmica resultante, é necessário efetuar um número suficiente de períodos de modulação, o que significa que as medições são demoradas.
Medição de CP com modulação de temperatura utilizando DSC
Ao determinar a capacidade térmica específica utilizando a medição com modulação de temperatura, uma onda sinusoidal é sobreposta à curva de temperatura. O pré-requisito para este método de medição é que o DSC possa seguir a temperatura modulada especificada. Por conseguinte, o perfil de temperatura [4, p. 132] pode ser descrito da seguinte forma:
Isto resulta no fluxo de calor de
com
[2, p. 187], o que significa que
Se a DSC medida for analisada, a capacidade térmica específica [1, p. 363] é calculada do seguinte modo
A inércia dos sistemas de medição e dos fornos limita a amplitude e exige longos períodos de duração. Para obter uma boa resolução da capacidade térmica resultante, é necessário efetuar um número suficiente de períodos de modulação, o que significa que as medições são demoradas.
Separação da parte reversível e irreversível do sinal DSC
Um sinal DSC pode ser dividido em um componente reversível (abreviado como REV a seguir) e um componente não reversível (abreviado como NONREV a seguir) de acordo com
pode ser separada [5, p. 172]. A parte reversível de um sinal DSC inclui os efeitos que ocorrem de forma reprodutível, tais como transições vítreas ou processos de fusão [2, secção 3.1.4]. Os efeitos irreversíveis são aqueles que ocorrem apenas uma vez na amostra correspondente, como a evaporação da água. Estes sinais podem ser separados uns dos outros através de medições com modulação de temperatura. De acordo com a fórmula de cálculo da medição com modulação de temperatura [5, p. 172], pode assumir-se que
Assim, a parte reversível pode ser descrita da seguinte forma
e a parte irreversível de um sinal DSC após
Se o sinal de medição modulado tiver sido registado e a capacidade térmica específica tiver sido calculada utilizando DSC, conforme descrito em Medição CP com modulação de temperatura, NONREV pode ser calculado de acordo com
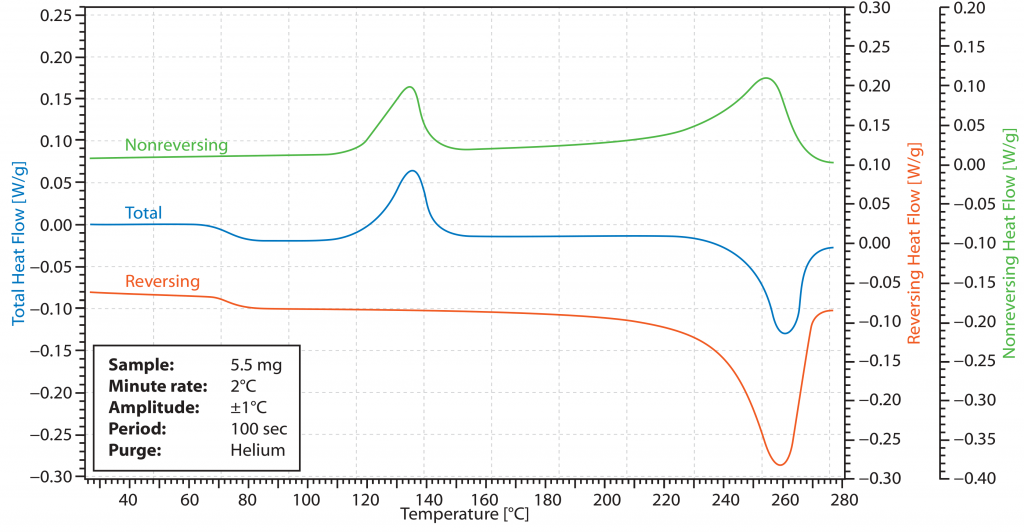
e, assim, calcula também o REV subtraindo o NONREV do sinal DSC. Se os efeitos se sobrepuserem a outras medições, podem muitas vezes ser claramente atribuídos e analisados utilizando esta separação. No entanto, o tempo e o trabalho envolvidos são significativamente maiores. A Fig. 3 mostra uma representação típica de um sinal DSC com componentes reversíveis e irreversíveis associados.
Medição do 3-Omega CP por DSC
Outro método para determinar a capacidade térmica específica é o método 3ω. O método inventado por David Cahill utiliza um aquecedor que é excitado com a velocidade angular ω. O método é utilizado para determinar a condutividade térmica [6, p. 19]. Esta é determinada por
e pode ser utilizado em conjunto com
pode ser convertido [6, p. 69]. Medindo a variação periódica da temperatura na amostra, é assim possível determinar o valor da capacidade térmica específica. No entanto, como o método foi concebido para medir amostras de película fina, que raramente são utilizadas em medições DSC convencionais, o método é dificilmente adequado para dispositivos DSC convencionais.
Podes determinar a capacidade térmica específica com os seguintes aparelhos de medição Linseis: Chip DSC , DSC PT 1600 (HDSC L62) , STA .
Literatura:
- B. Wunderlich, Thermal Analysis of Polymeric Materials (Análise Térmica de Materiais Poliméricos). Berlim, Heidelberg: Springer-Verlag Berlin Heidelberg, 2005.
- S. M. Sarge, G. W. H. Höhne e W. Hemminger, Calorimetry: Fundamentals, instrumentation and applications. Weinheim, Alemanha: Wiley-VCH Verlag, 2014.
- G. W. H. Höhne, W. Hemminger e H.-J. Flammersheim, Differential Scanning Calorimetry: An Introduction for Practitioners. Berlim, Heidelberg: Springer, 1996.
- G. W. H. Höhne, W. F. Hemminger e H.-J. Flammersheim, Differential Scanning Calorimetry, 2nd ed., Berlin, Heidelberg: Springer, 2003. Berlim, Heidelberg: Springer, 2003.
J. D. Menczel e R. B. Prime, Thermal analysis of polymers. Hoboken, N.J: John Wiley, 2009. - P. Böckh e T. Wetzel, Wärmeübertragung: Fundamentals and Practice, 5.ª ed. Berlim: Springer Vieweg, 2014.
