Índice
¿Qué son los materiales termoeléctricos?
Los materiales termoeléctricos pueden convertir directamente el calor en energía eléctrica.
Esta propiedad se basa en el efecto Seebeck en el que una diferencia de temperatura aplicada a un material genera una tensión.
Lo contrario es el efecto Peltier, que suele utilizarse para enfriar.
Un tercer efecto termoeléctrico es el efecto Thomson, que describe el transporte de calor a lo largo de un conductor de corriente en el que existe un gradiente de temperatura.
Debido a la posibilidad de utilizar directamente la energía térmica, los materiales termoeléctricos se han convertido en el centro de la investigación y el desarrollo.
Por un lado, pueden utilizarse para generar energía eléctrica a partir de fuentes de energía primaria; por otro, resulta tentador generar electricidad a partir de calor residual, conservando así los recursos de combustibles fósiles y reduciendo al mismo tiempo la emisión de CO2.
Dado que la tensión eléctrica inducida por el efecto Seebeck es muy pequeña (normalmente de unos pocos a unos cientos de μV/K), se están realizando grandes esfuerzos para desarrollar materiales termoeléctricos mejorados.
Los materiales termoeléctricos clásicos proceden del grupo de los semimetales y semiconductores (IV a VI grupo principal de la tabla periódica) o son aleaciones de materiales de estos grupos, ya que en ellos el coeficiente Seebeck es especialmente elevado.
El efecto Seebeck puede aumentarse aún más mediante el dopaje.
¿Qué es la cifra de mérito?
En general, una cifra de mérito es una medida de la idoneidad de los materiales, métodos o equipos en comparación con otras alternativas.
La figura de mérito figura de mérito «ZT describe la idoneidad de los materiales termoeléctricos y se define de la siguiente manera:
Ecuación 1
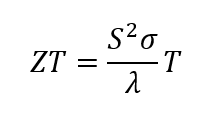
Los materiales termoeléctricos deben tener baja conductividad térmica y alta conductividad eléctrica además de un coeficiente Seebeck lo más grande posible.
Los materiales de alta conductividad térmica no permiten grandes gradientes de temperatura; si la conductividad eléctrica es baja, no se pueden obtener corrientes útiles.
Además, la figura de mérito y la diferencia de temperatura están directamente relacionadas con la eficiencia η de un dispositivo termoeléctrico, por lo que ésta aumenta cuando ZT y ΔT tienen valores grandes.
Ecuación 2
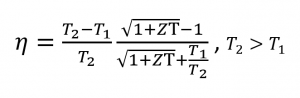
Optimización de los materiales termoeléctricos
Una gran variedad de clases de materiales presentan efectos termoeléctricos de distinta intensidad.
Durante mucho tiempo, se consideró que un valor de 1 era la cifra máxima de mérito, pero hoy en día algunos materiales optimizados alcanzan valores de alrededor de 2 o superiores.
Como puede verse en la ecuación 1, hay dos enfoques diferentes para aumentar ZT: o bien se puede maximizar el factor de potencia S2σ, y/o la conductividad térmica puede minimizarse.
Para conseguirlo, se mejoran los materiales existentes, por ejemplo dopándolos, y se desarrollan nuevos materiales.
Esto último puede conseguirse, por ejemplo, mediante nanoestructuración, ya que así se reduce en gran medida la conductividad térmica sin influir mucho en el factor de potencia.
Si se utilizan termoeléctricos en la industria, el coste, la toxicidad y la disponibilidad de los materiales son consideraciones clave.
Medición de la figura de mérito
Existen varios métodos para determinar la figura de mérito termoeléctrica.
- En primer lugar, se pueden medir los parámetros individuales (coeficiente Seebeck, conductividad eléctrica y térmica) y calcular ZT según la ecuación 1.
- Por otra parte, es posible determinar ZT directamente mediante el método de Harman.
1. Cálculo de la ecuación 1
Existen varios dispositivos comerciales para medir casi simultáneamente la conductividad eléctrica y el coeficiente Seebeck.
La conductividad térmica o la difusividad termica suele determinarse por el método del láser o del flash de luz.
El resultado directo de este método es la difusividad térmica, si se conocen la densidad y la capacidad calorífica específica.
La conductividad térmica puede calcularse a partir de ella mediante la siguiente fórmula:
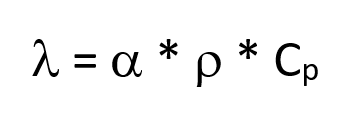
Todas estas variables dependen de la temperatura
Por tanto, hay que determinar un total de cinco variables (dependientes de la temperatura) para calcular la figura de mérito. Puedes encontrar un análisis de errores en la bibliografía [1].
2. Determinación con el método Harman
El método Harman permite medir directamente la figura de mérito.
Se consigue haciendo pasar una pequeña corriente a través de una muestra en forma de varilla en condiciones adiabáticas.
La caída de tensión observada se compone de un componente óhmico (UR; resistencia eléctrica) y un componente termoeléctrico causado por el efecto Seebeck (Uth; tensión térmica).
A diferencia de la componente óhmica, que se produce espontáneamente, la causada por el efecto Seebeck se acumula lentamente:
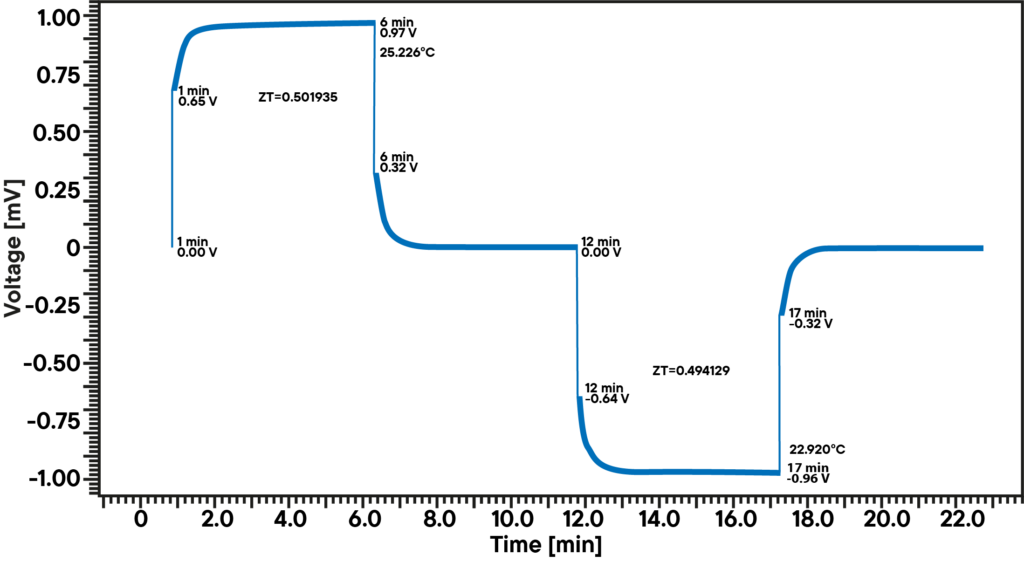
La cifra de mérito se obtiene dividiendo los dos componentes:
Ecuación 4
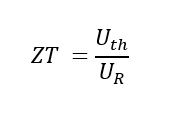
Literatura:
[1] A. Alleno et al., A round robin test of the uncertainty on the measurement.of the thermoelectric dimensionless figure of merit of Co0.97Ni0.03Sb3, REVISIÓN DE INSTRUMENTOS CIENTÍFICOS 86, 011301 (2015).
[2] T.C. Harman, Journal of Applied Physics 29, 1373 (1958).
[3] T. C. Harman, J. H. Cahn y M. J. Logan, J. Appl. Phys. 30(9), 1351 (1959).
