目次
熱電材料とは?
熱電材料は熱を直接電気エネルギーに変換することができる。
この特性は ゼーベック効果材料に温度差をつけると電圧が発生する。
この逆はペルチェ効果で、通常は冷却に使われる。
第3の熱電効果はトムソン効果で、温度勾配が存在する通電導体に沿った熱輸送を説明する。
熱エネルギーを直接利用できることから、熱電材料が研究開発の焦点となっている。
一方では、一次エネルギー源から電気エネルギーを生成するために使用することができ、他方では、廃熱から電気を生成することで、化石燃料資源を節約し、同時にCO2の放出を削減することができる。
ゼーベック効果によって誘起される電気電圧は非常に小さい(通常、数〜数百μV/K)ため、改良された熱電材料の開発に大きな努力が払われている。
古典的な熱電材料は、半金属や半導体のグループ(周期表のIV族からVI族)に属するか、これらのグループの材料の合金である。
ゼーベック効果は、ドーピングによってさらに増大させることができる。
功労者とは?
一般に、メリットとは、代替品と比較した材料、方法、設備の適合性を示す尺度である。
サーモエレクトリック ZT “はは熱電材料の適合性を表し、以下のように定義される:
式1
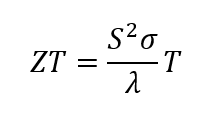
熱電材料は、熱伝導率が低く、電気伝導率が高くなければならない。 高い電気伝導率ゼーベック係数ができるだけ大きいこと。熱伝導率の高い材料は大きな温度勾配を許さず、電気伝導率が低ければ有用な電流は得られない。
さらに、メリット指数と温度差は、熱電素子の効率ηに直接関係するため、ZTとΔTが大きな値になると効率ηは増加する。
式2
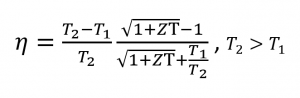
熱電材料の最適化
多種多様な材料が異なる強さの熱電効果を示す。
長い間、1という値が最大のメリットと考えられてきたが、今日、最適化された材料の中には2またはそれ以上の値を達成するものもある。
式1からわかるように、ZTを増加させるには2つの異なるアプローチがある。 熱伝導率を最小にすることができる。これを達成するために、例えばドーピングによって既存の材料を改良したり、新しい材料を開発したりする。後者は、例えばナノ構造化によって達成することができ、これによって力率に大きな影響を与えることなく熱伝導率を大幅に低減することができるからである。サーモエレクトリックが産業界で使用される場合、コスト、毒性、材料の入手性が重要な考慮事項となる。
メリット・フィギュアの測定
熱起電力係数の決定には様々な方法がある。
- まず、個々のパラメータ(ゼーベック係数、電気伝導率、熱伝導率)を測定し、式1に従ってZTを計算することができる。
- 一方、ZTをハーマン法で直接決定することも可能である。
1.式1の計算
熱伝導率は、以下の式によって算出することができる:
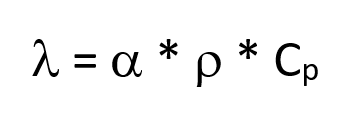
これらの変数はすべて温度に依存する
従って、功利値を計算するためには、合計5つの(温度に依存する)変数を決定する必要がある。 誤差解析は文献[1]に記載されている。
2.ハルマン法による決定
ハーマン法では、功利指数を直接測定することができる。 これは、断熱条件下で棒状の試料に小電流を流すことで実現します。 観測される電圧降下は、オーミック成分(UR:電気抵抗)とゼーベック効果による熱電成分(Uth:熱電圧)から構成されます。 自発的に発生するオーミック成分とは対照的に、ゼーベック効果によるものはゆっくりと蓄積する:
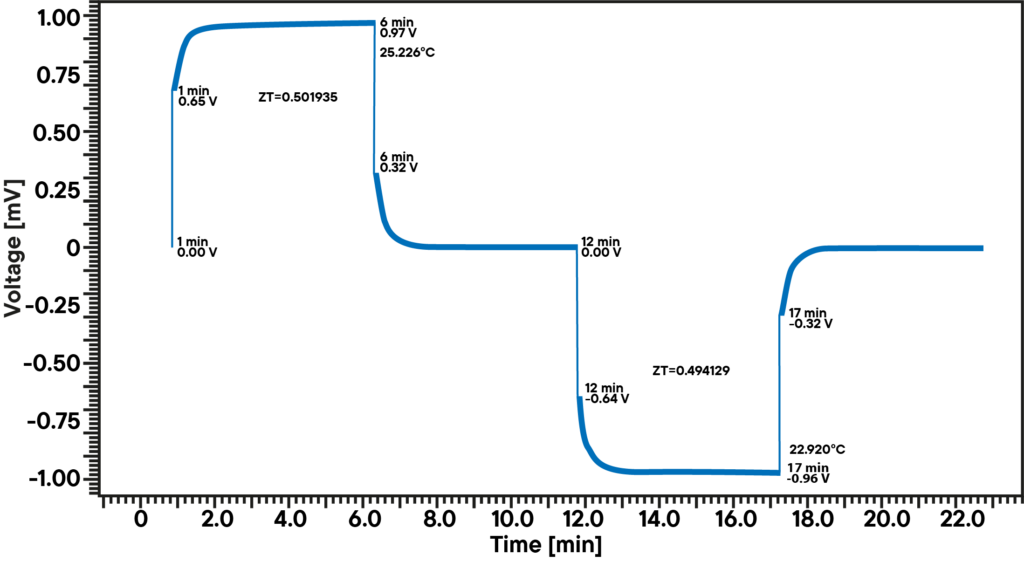
メリットの数値は、2つの成分を割って得られる:
式4
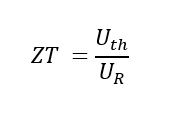
文学:
[1] A. Alleno et al., A round robin test on measurement.of thermoelectric dimensionless figure of merit of Co0.97Ni0.03Sb3, REVIEW OF SCIENTIFIC INSTRUMENTS 86, 011301 (2015).
[2] T.C. Harman, Journal of Applied Physics 29, 1373 (1958).
[3] T. C. Harman, J. H. Cahn, and M. J. Logan, J. Appl. Phys. 30(9), 1351 (1959).