Elastic modulus of Thermal Analysis
Modul of elasticity | Young’s modulus
The modulus of elasticity is a frequently required material parameter in the static calculation of components. If a tensile force acts on a solid body, it reacts with a change in length. Inner forces are created in the body, which reverse the change in length as soon as the external pulling force ceases. If the size of the tensile force lies below a material-dependent limit value, the force and change in length are proportional to one another. This relationship is known as Hooke’s Law.
In order to achieve comparable results, the tensile force is related to the cross-sectional area of the unloaded component. The quotient of force and cross section is the tension.
The change in length is related to the length of the unloaded component for the same reason. The quotient of the length increase and the original length is the elongation.
What is the Young´s modulus?
Young’s modulus, or the Young modulus, is a mechanical property that measures the stiffness of a solid material. It defines the relationship between stress (force per unit area) and strain (proportional deformation) in a material in the linear elasticity regime of a uniaxial deformation. The value is given in the unit of measure N / m².
This unit of measurement is mathematically consistent with the unit of measure Pascal used for the physical size of pressure. In some tables, this unit of measurement is also used for the modulus of elasticity.
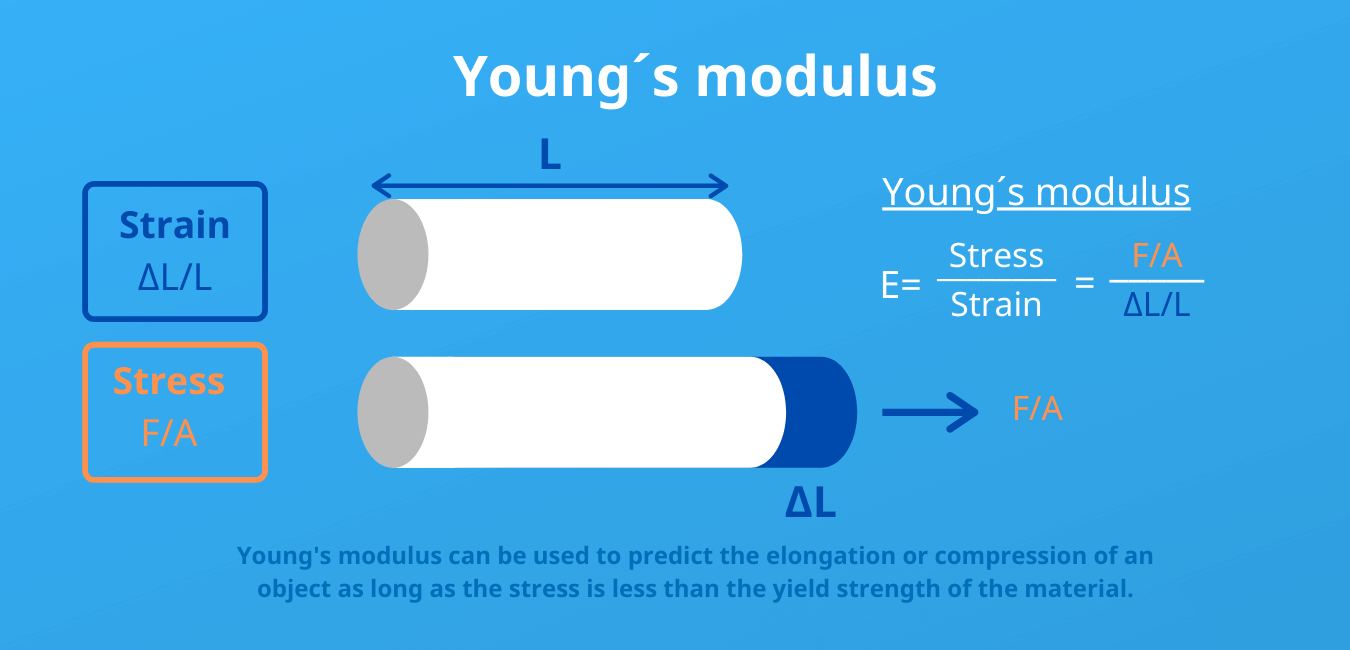
The Young´s modulus is a specific form of Hooke’s law of elasticity
The determination of the modulus of elasticity takes place in the context of a tensile test. In the tensile test, a specimen is loaded with precisely defined dimensions by a growing tensile force until the specimen tears. The result is a characteristic of the material stress-strain diagram. From the curve in this diagram, the modulus of elasticity and the tensile strength can be calculated. Further characteristics are the elastic limit, the elongation at break and the fracture constriction.
The conditions for the tensile test are specified in different standards for the different material groups. It is taken into account that, for example, metals, plastics, adhesives or textile fibers react differently to tensile stresses.
International standards:
ASTM E111 – 17 Standard Test Method for Young’s Modulus, Tangent Modulus, and Chord Modulus
